Inscription / Connexion Nouveau Sujet
Continuité d'une fonction partie entière.
Bonjour,
Voici l'énoncé de mon exercice:
On considére les fonctions f et g définies sur  par:
par:
x

 , f(x)=x+
, f(x)=x+ (x-E(x)) et g(x)=E(x)+
(x-E(x)) et g(x)=E(x)+ (x-E(x))
(x-E(x))
Où la notation E(x) désigne la partie entière de x
Dans les questions, la lettre n désigne un entier arbitraire.
1. Justifier que f et g sont continues sur l'intervalle ]n,n+1[
2.a) Etudier la continuité de f et g en n
2.b) Conclure concernant la continuité sur  de f et g
de f et g
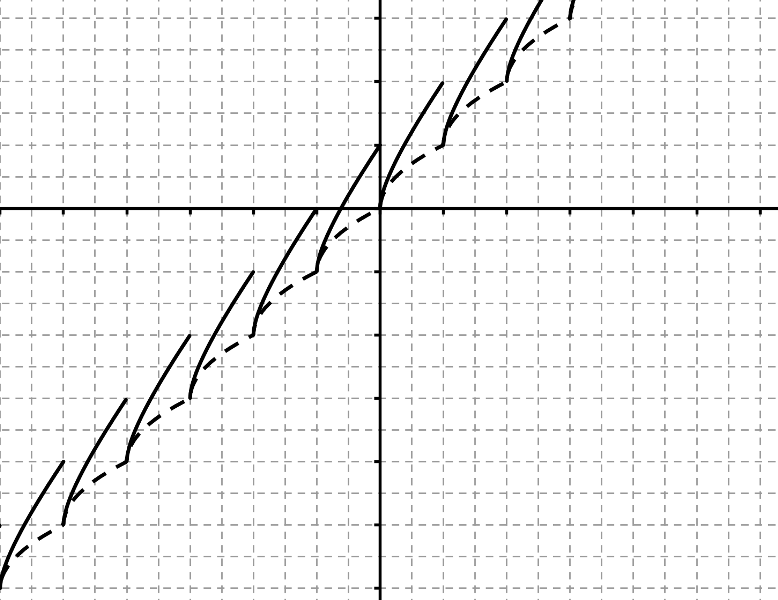
3. Représenter sur le même graphique en limitant les abscisses à l'intervalle [-1,2]
Mes réponses :
1. La fonction partie entière est continue sur ]n,n+1[.
Donc les fonctions f et g sont continues sur cet intervalle puisque c'est la composé de fonction continue sur cet intervalle.
2.a) Ici ce pose le problème, j'avais débuter mon raisonnement avec un entier naturel , de ce fait j'avais conclue que f n'est pas continue en n et g est continue en n.
Mais le problème ce que n est un entier arbitraire donc peut être négatif (non?)
Donc comment procédé pour cette question? faut-t-il que je disqtingue les deux cas où il faut tout refaire ?
Pour le reste des questions j'attendrais l'aide a la question 2a.
Merci 
Le fait que l'entier n soit positif ou négatif est sans intérêt ici, car la fonction E(x) a la même définition quel que soit le signe de x :
E(x) est l'unique entier tel que E(x)  x < E(x)+1
x < E(x)+1
IL n'y a aucune différence entre le raisonnement à faire lorsque n est un entier naturel et le raisonnement à faire lorsque n est un entier négatif. Pour ton raisonnement, il suffit de ne pas préciser que n est "naturel", normalement, rien dans ton raisonnement (que je n'ai pas vu) ne s'oppose à ce que n soit négatif !
A oui tu a pas tord pythamede.
Bon voici mon raisonnement pour montrer la continuité de f et g en n :
Commençons par f :
Pour montrer que la fonction est continue en un point eu montre que la limite a gauche et la limite a droite sont identiques.
= n+1 pour limite à gauche.
= n pour limite à droite.
Donc f n'est pas continue en n.
Puis pour g :
a gauche =
a droite =n
Donc g est continue en n
Mon raisonnement semble faut, puisque pour al question 2B cela ne pourra pas répondre à la question n'est-ce pas?
Quelqu'un peut m'éclairais Svp ?
Merci
salut
ben quel est le pb ?
f n'est pas continue en les entiers donc f n'est pas continue
g est continue entre les entiers et en les entiers donc g est continue....
Bien que dois-je répondre à la question 2B alors ?
Il faut que je réponde que f et g ne sont pas continue sur  ?
?
A donc il faut dire que f n'est pas continue sur R car n'est pas compris entre des entiers et g est continue sur R car il est compris entre des entiers ?
Il faut juste dire sa ? 
f n'est pas continue sur R car pas continue en les entiers
g est continue sur R (car continue entre les entiers et en les entiers !!!!)
Je suis troublé par cet exercice^^"
Déjà ais-je bon sur la continuité de mes fonction car si c'est déjà pas bon sa sert a rien de continuer.
Je ne comprend pas trop pourquoi g continue avec votre réponse carpediem ( entre les entiers et en les entiers )
Et ensuite pour tracer la courbe il faut juste prendre différent valeurs de X ?
Merci
sur chaque intervalle ]n,n+1[ f et g sont continues comme composée de fonctions continues commme tu l'as dit
maintenant en un entier n tu as prouvé que f n'est pas continue et g est continue
d'où la conclusion...
OK merci Carpediem je crois que je comprend petit à petit 
Donc pour la courbe , je sais que g est continue donc pas de problème, mais par contre f n'est pas continue , cela veut dire qu'a chaque entier je doit "lever mon crayon" ?
Merci pour le dessin, carpediem, je n'ai pas cherché à imaginer à quoi resssemblait les graphes.
Pour montrer que la fonction est continue en un point eu montre que la limite a gauche et la limite a droite sont identiques.
Certes, cela est nécessaire pour que la fonction soit continue, mais cela ne suffit pas. Il faut de plus que
Il convient de ne pas oublier ce détail.
Par contre, il suffit de trouver une seule valeur de a de x telle que la limite à gauche de f en a soit différente de la limite à droite pour pouvoir affirmer que f n'est pas continue sur
mais par contre f n'est pas continue , cela veut dire qu'a chaque entier je doit "lever mon crayon" ?
L'expression "lever (ou pas) son crayon" est une explication valable pour un élève de première, à la rigueur de Terminale. Mais en à mon sens, en math'sup', la manière de tenir son crayon ne devrait pas intervenir dans les raisonnements mathématiques.
Un fonction f est continue en a si
1 - f(a) est défini
2 -
3 -
Il arrive cependant que l'on condense, de manière correcte, cette définition en disant :
f est continue en a si
Que dire à part MERCI 
pythamede merci de votre explication, mais je voulais abrégé mon explication , en tout cas joli explication qui est très significative 
Merci également a carpediem pour ce graphe 
Je l'avais tracé sur WIMS mais pour les lui les courbes étaient continues sont les points se rejoignées.
Bonne Continuation Merci 



 analyse en post-bac
analyse en post-bac