Inscription / Connexion Nouveau Sujet
Continuité et continuité uniforme
Bonsoir, j'étais en train de relire mon cours d'analyse et je n'arrive pas à comprendre la différence entre la continuité et la continuité uniforme.
Dans mon cours la continuité en un point x0 est définie par
>0,
>0 |x-x0|< => | f(x)-f(x0) | <
Et du coup f est continue sur I si f est continue en tout point de I
Et la continuité uniforme sur I est définie par
>0,
>0 (x,y)
IxI |x-y|< => | f(x)-f(y) | <
A première vue la différence est qu'on parle de continuité uniforme sur un intervalle, sur un point x0 ça n'a pas de sens et je sais que la continuité uniforme sur I implique la continuité sur I
Par contre graphiquement, quelle est la différence une fonction continue sur I et une fonction continue uniformément sur I ?
J'ai l'impression que par exemple la fonction exponentielle n'est pas uniformément continue sur [0,+inf[ parce que l'image de l'intervalle [x-,x+] par la fonction exponentielle devient beaucoup trop large
Merci d'avance
Bonsoir,
Par contre graphiquement, quelle est la différence une fonction continue sur I et une fonction continue uniformément sur I ?
La fonction continue peut se tracer sans lever le crayon.
Pour la fonction uniformément continue, on utilise rarement une interprétation géométrique, mais si tu en veux une, imagine le graphe de la fonction. Alors pour un rectangle de hauteur quelconque (longueur selon l'axe Oy), tu peux toujours adapter sa largeur (longueur selon l'axe Ox) (et une fois que tu l'as fait, tu n'y touches plus), tel que si tu translates ce rectangle le long de l'axe (Ox), tu peux toujours, quitte à changer sa position selon l'axe (Oy), faire en sorte que la courbe de f ne sorte du rectangle que par les côtés droite ou gauche, et jamais par le haut ou par le bas du rectangle.
Personnellement, je trouve l'interprétation graphique inexploitable. Pour moi, l'uniforme continuité signifie simplement que si deux points sont proches, alors leurs images sont proches. Pour la continuité, les termes "proches" sont à redéfinir selon chaque point auquel on se trouve.
J'ai l'impression que par exemple la fonction exponentielle n'est pas uniformément continue sur [0,+inf[ parce que l'image de l'intervalle [x-
,x+] par la fonction exponentielle devient beaucoup trop large Oui, si on veut.
D'accord je vois, par contre j'ai un autre soucis plus concret cette fois
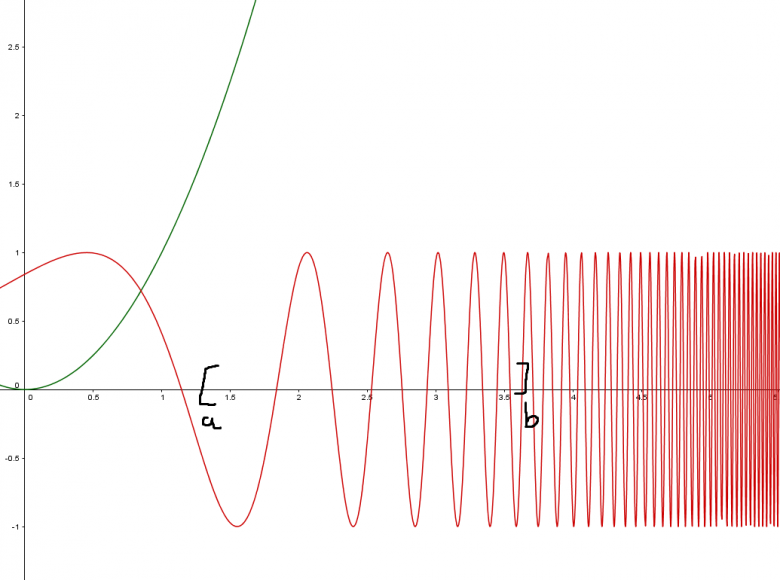
En fait sur ce graphe j'ai tracé x^2 en vert et cos(exp(x)) en rouge, elles sont clairement continues sur R et elles ne sont pas uniformément continues sur R.
Par contre, sur le compact [a,b], elles sont uniformément continues d'après le théorème de Heine. Mais ce que je ne comprends pas c'est pourquoi on n'a pas " si deux points sont proches, alors leurs images sont proches. " avec x^2 on se retrouve avec la même situation qu'avec l'exponentielle tout à l'heure finalement
Ou bien justement, vu qu'on se place sur un compact, on peut choisir un delta qui fonctionne tout le temps ?
En gros, pourquoi est-ce que le théorème de Heine fonctionne, pourquoi est-ce que là, sur le compact, les fonctions sont uniformément continues?
Si on prend l'exemple de la fonction carré, pour commencer.
donc en notant
,
Or tout l'objet de la continuité uniforme est de majorer la différence , avec un contrôle sur la quantité
. Clairement, ici la majoration échoue si
n'est pas contrôlé. Or, en se limitant à un segment, il s'agit d'une quantité bornée, et la majoration fonctionne.
Pour le cas de la fonction , c'est peut-être un peu moins facile à écrire. En regardant le dessin, on voit bien que le problème est que les oscillations deviennent de plus en plus rapides, d'amplitude constante. Il faut de moins en moins de temps pour passer de -1 à 1. Imaginons que l'on ait
, alors, si on s'autorise d'aller aussi loin qu'on veut vers la droite, on trouvera des oscillations suffisamment rapides pour que l'on passe de -1 à 1 en un temps plus faible que
, ce qui contredit l'uniforme continuité. En revanche, en se limitant à un segment, on contrôle la rapidité des oscillations.
Annuler
connectez vous
analyse en post-bac