Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

convergence

Posté par Djeffrey (invité) 19-10-05 à 18:43

Bonjour, j'ai un nouveau souci pour ce chapitre affreux des series numeriques (a mort !), pourriez vous m'aider svp...

Soit f une fonction de R+ dans R+ decroissante, on pose u_n=f(n) et s_n=u_0+...+u_n.

Montrer que la suite de terme general s_n-\Bigint_0^{n+1} f(t) dt est convergente. Donner une interpretation graphique de ce fait.
Application : On pose \gamma=lim(1+\frac{1}{2}+...+\frac{1}{n}-ln(n)). Justifier l'existence de \gamma et montrer que \frac{1}{2}\le\gamma\le1

Voila j'imagine que ce n'est pas si compliqué mais la sur ce chapitre je suis a la ramasse...
Merci a tous si vous pouvez m'aider
Merci

Posté par
ottore : convergence 19-10-05 à 18:45

Bonjour,
en effet ce n'est pas compliqué, si ta fonction est décroissante elle est intégrable (ce serait déjà bien de s'en rendre compte parce qu'on l'intègre...)
Ensuite, si tu intègres sur chacun des intervalles de longueur 1, tu peux facilement encadrer ton intègrale par des sommes et inversement.
Fait un dessin pour t'aider, et regarde ce que tu peux dire de ton intègrale par rapport a Sn et Sn+1

Posté par Djeffrey (invité)re : convergence 19-10-05 à 19:05

je pense encadrer l'integrale entre Sn et Sn+1 avec le dessin que j'ai fait, est ce correct?

Posté par Djeffrey (invité)re : convergence 19-10-05 à 20:57

Si otto ne repase pas est ce que quelqu'un pourrait me dire si c'est bon, et si possible m'aider a avancer dans l'exo parce que j en'y arrive ps mieux...

Merci a tous

Posté par
Roulianere : convergence 19-10-05 à 21:10

C'est ça, le principe c'est d'enncadrer ton intégrale ....

je te fais le début :

f étant décroissante sur R+ alors, t[k,k+1], f(k+1)f(t)f(k)

En intégrant entre k et k+1, on a alors :

f(k+1)\int_k^{k+1} f(t) dt f(k)

Ensuite, tu sommes entre 0 et n

Mais je pense que c'est ce que tu as fait



Posté par Djeffrey (invité)re : convergence 19-10-05 à 21:42

oui c'est exactement ce que j'ai fait suite au conseil d'otto.
Mais ensuite comment dois je faire pourtrouver que la suite avec la difference converge?

Posté par
Roulianere : convergence 19-10-05 à 21:51

Tu as sommé ou pas de 0 à n ?

Tu devrais arriver à :


S_{n+1}\int_0^{n+1} f(t) dt S_n si je n'ai pas fait d'erreur ....

Ensuite, essaye d'encadrer S_n-\int_0^{n+1} f(t) dt

Posté par Djeffrey (invité)re : convergence 20-10-05 à 16:51

oui je trouve bien ca Nicoco et ensuite j'ai ecris 0\le S_n-\Bigint_0^{n+1} f(t) dt\le S_n
Est ce que cela me suffit pour dire que la suite de terme general S_n-\Bigint_0^{n+1} f(t) dt converge ?
J'en sais trop rien en fait...

Sinon pour l'interpretation graphique je pense que cela traduit un ecart quasi constant entre les deux suites a partir d'un certain rang, c'est bien cela??

Pour l'application selon moi il s'agit de bien dire que la fonction inverse est decroissante etc...
Par contre l'integrale ne peut pas commencer a 0 (ni la suite) et on trouve 1+\frac{1}{2}+...+\frac{1}{n}-ln(n+1) avec la formule... Donc ca m'embete un peu. et pr l'encadrement de gamma c'est pas mieux

Donc est ce que qqn peut rentrer un peu plus dans les details pour m'aider a finir cet exo svp, ca serait tres sympa...
Merci

Posté par
Roulianere : convergence 20-10-05 à 18:09

J'ai fait une petite erreur au message de 21:51, on doit plutot trouver comme encadrement :

S_{n+1}-f(0) \int_0^{n+1} f(t) dt S_n

On a alors :

U_{n+1}-f(0)\int_0^{n+1} f(t) dt - S_n0

Et là, je vois pas comment on en déduit la convergence ?

( U_{n+1} va bien tendre vers 0, on il nous reste du f(0) )

J'ai du faire une erreur quelque part ....

Posté par
elhor_abdelali Correcteurre : convergence 20-10-05 à 19:22

Bonjour;
(*)En partant du résultat de Nicoco on a que:
0\le\underb{s_n-\int_{0}^{n+1}f(t)dt}_{3$ a_n}\le f(0)-f(n+1)\le f(0)
a_{n+1}-a_n=f(n+1)-\int_{n+1}^{n+2}f(t)dt\ge0
d'où (a_n) croissante majorée donc convergente.
(*)Pour l'application partir de 1 et non de 0.
Sauf erreurs bien entendu

Posté par
Roulianere : convergence 20-10-05 à 19:47

Merci Elhor, par contre, je vois pas pourquoi  f(n+1)-\int_{n+1}^{n+2} f(t) dt\ge0 ?

Posté par
elhor_abdelali Correcteurre : convergence 20-10-05 à 19:56

Comme f est décroissante on a:
3$\fbox{\forall t\in[n+1,n+2]\\f(n+2)\le f(t)\le f(n+1)} d'où par intégration 3$\fbox{f(n+2)\le\int_{n+1}^{n+2}f(t)dt\le f(n+1)} et donc que:
3$\fbox{f(n+1)-\int_{n+1}^{n+2}f(t)dt\ge0

Posté par
Roulianere : convergence 20-10-05 à 19:58

Ben oui, évidemment, honte à moi

Merci

Posté par Djeffrey (invité)re : convergence 20-10-05 à 20:05

merci bien elhor c'est tres clair.
Pour ce qui est de l'interpertation graphique j'imagine que si personne n'a contredit c'est que c'est bien ce a quoi je pensais, c'est ca?

Posté par
elhor_abdelali Correcteurre : convergence 20-10-05 à 21:35

Bonsoir;
On peut aussi remarquer que:
3$\fbox{s_n-\int_{0}^{n+1}f(t)dt=\Bigsum_{0}^{n}(u_k-\int_{k}^{k+1}f(t)dt)} et comme 3$\fbox{\forall k\in\mathbb{N}\\u_{k+1}\le\int_{k}^{k+1}f(t)dt\le u_k} on voit que 3$\fbox{\forall k\in\mathbb{N}\\0\le u_k-\int_{k}^{k+1}f(t)dt\le u_k-u_{k+1}} ce qui montre que la suite (s_n-\int_{0}^{n+1}f(t)dt)_n peut ^tre vue comme une série à termes positifs majorée par une autre convergente (vers u_0-\lim_{x\to+\infty}f(x)).
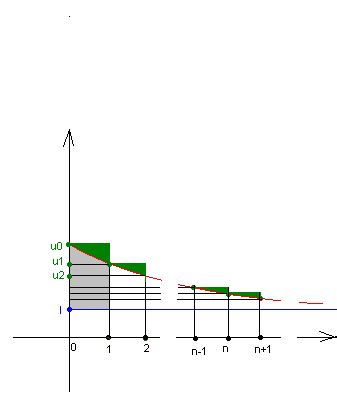
Pour l'interpretation graphique,je pense que ça doit ^tre une illustration de ce fait:
Notons 2$\blue\fbox{l=\lim_{x\to+\infty}f(x)}
Les parties vertes sur le dessin représentent les 2$\fbox{u_k-\int_{k}^{k+1}f(t)dt} et on voit bien qu'en les translatant vers le premier rectangle (rectangle gris) leur sommme à l'infini est inférieure ou égale à l'aire de celui ci qu'est u_0-l.

convergence

Posté par
Roulianere : convergence 20-10-05 à 23:17

Merci pour toutes ces précisions !

Posté par Babou14 (invité)re : convergence 21-10-05 à 02:43

s'appelle la constante d'Euler, en passant

Posté par
elhor_abdelali Correcteurre : convergence 21-10-05 à 16:58

Bonjour;
Pour l'application considérons la fonction 3$\fbox{f{:} {\mathbb{R}}^+\to{\mathbb{R}}^+\\x\to\frac{1}{x+1}} on a bien 3$\fbox{f\hspace{5}decroissante\\l=\lim_{x\to+\infty}f(x)=0} d'où:
la suite (a_n=s_n-\int_{0}^{n+1}f(t)dt=1+\frac{1}{2}+..+\frac{1}{n+1}-ln(n+2))_{n\ge0} croit vers un réel \gamma\in[a_5,u_0-l]=[\frac{147}{60}-ln(7),1]\subset[\frac{1}{2},1]
Pour conclure il suffit de voir que la suite (b_n=1+\frac{1}{2}+..+\frac{1}{n}-ln(n))_{n\ge1} a la m^me limite que (a_n).

Remarques:
(*)Comme l'a mentionné Babou14,la constante \gamma est connue sous le nom de "constante d'Euler" et on ignore toujours si cette constante d'Euler (1781) est: rationnelle, irrationnelle,algébrique ou transcendante et si,un jour, on trouvera une fraction rationnelle(\gamma=a/b),alors b est supérieur à 10 244 663.
(*)\gamma = 0,577 215 664 901 532 860 606 512 090 082 402 431...

Sauf erreurs bien entendu


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !