Inscription / Connexion Nouveau Sujet
courbe
bonjour, j'aurais besoin pour cet exo, merci.
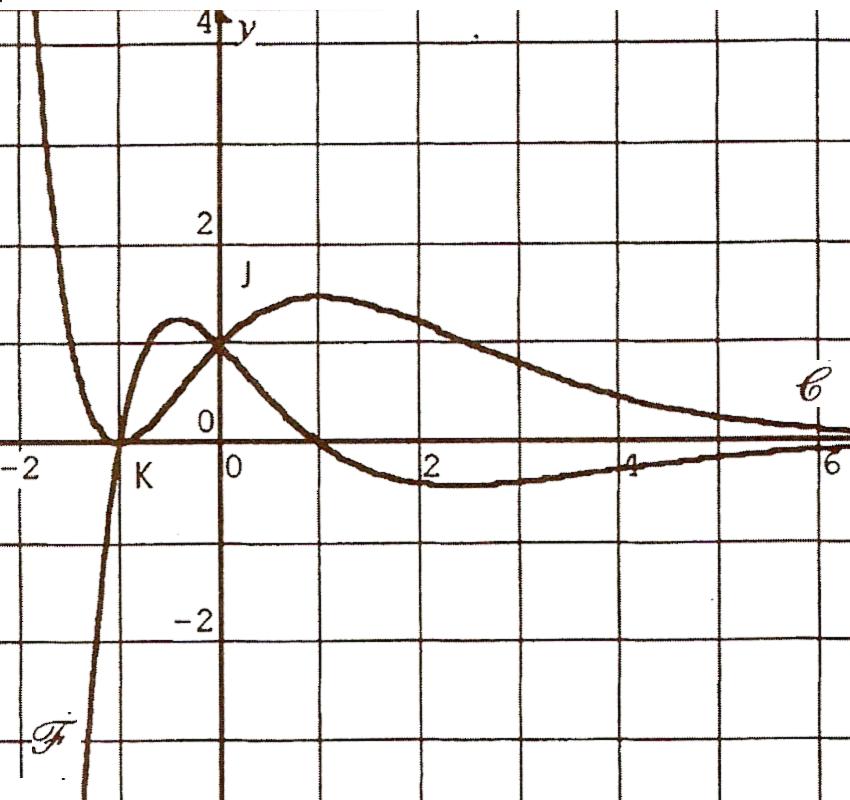
On donne dans un repère orthogonal, les courbes C et F représentatives de deux fonctions définies et dérivables sur R. On sait que l'une de ces fonctions est la fonction dérivée de l'autre ; on peut donc les noter g et g'. En outre, ces deux courbes passent par le point J(0;1) et K(-1;0).
a)Associer à chacune des fonctions g et g' sa représentation graphique.
b)Quel est le coefficient directeur de la tangente à C au point d'abscisse 0 ?
a)
représentation grahique de g: courbe C
représentation grahique de g': courbe F
b)
on calcul Yj-Yk/Xj-Xk ?
Soit ça (mais je ne pense que c'est ce que l'on attend).
En utilisant ce que tu viens de trouver
C f et C f'
en plus tu as J(0;1) et K(-1;0)
Il faudrait que tu trouves, en fait, f'(0) tu es d'accord ? Car c'est le coefficient directeur de la tangente pour x = 0
Bonjour, j'aurais besoin d'aide pour cetteexo, merci.
partie A : lecture graphique
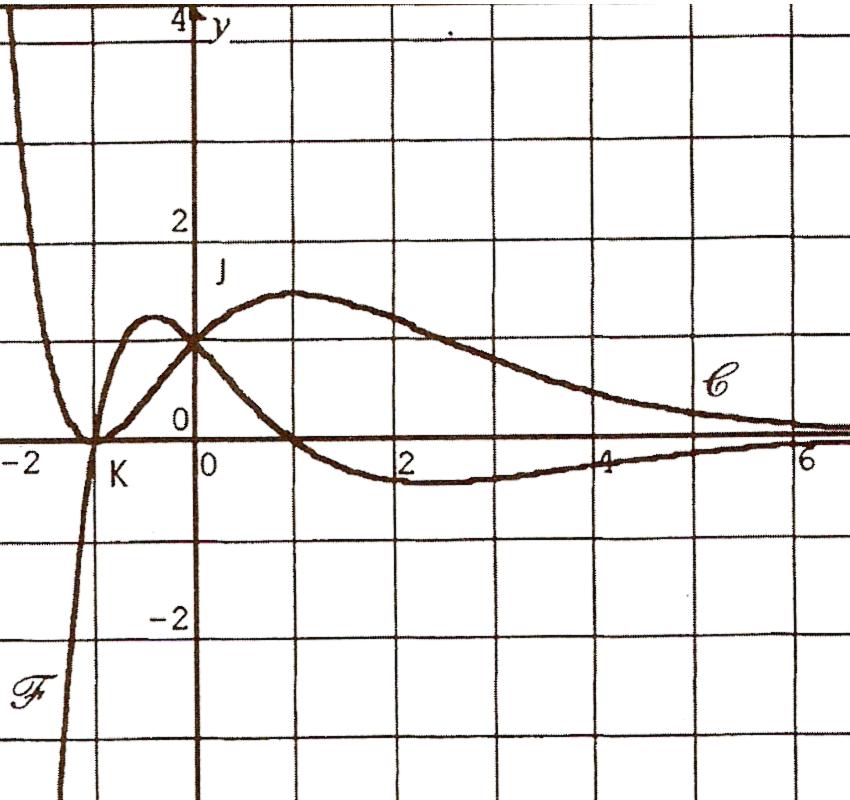
On donne dans un repère orthogonal, les courbes C et F représentatives de deux fonctions définies et dérivables sur R. On sait que l'une de ces fonctions est la fonction dérivée de l'autre ; on peut donc les noter g et g'. En outre, ces deux courbes passent par le point J(0;1) et K(-1;0).
a)Associer à chacune des fonctions g et g' sa représentation graphique.
b)Quel est le coefficient directeur de la tangente à C au point d'abscisse 0 ?
partie B
Soit l’équation différentielle (E): y'+ y = 2(x+1)e-x
a)Montrer que la fonction f0 définie sur R par:
f0(x)=(x²+2x)e-x est une solution de l'équation (E).
b)Résoudre l’équation différentielle (E') y'+ y = 0.
c)Soit u une solution de (E'). Montrer que f0+u est une solution de (E). On admettra que réciproquement, toute solution f de (E) est de la forme f = f0+u où u est une solution de (E'). En déduire pour x réel, l’expression de f(x)lorsque f est solution de (E).
d)Sachant que la fonction g de la partie A est solution de (E), déterminer g(x) pour x réel.
e)Déterminer la solution h de l’équation (E) dont la représentation graphique admet au point d’abscisse 0 une tangente de coefficient directeur 0.
partie C:
f est la fonction numérique définie sur R par: f(x)=(x²+2x+2)e-x
1)Étudier les limites de f en + et -
et - .
.
2)On sait que f est dérivable sur R; déterminer sa fonction dérivée et étudier son signe.
Donner le tableau de variations de f.
3)Dans un repère orthonormal (o;i;j), (unité graphique : 2 cm), on note C' la représentation graphique de f.
a)Déterminer une équation cartésienne de la tangente T à C' au point A d'abscisse -1.
b)Tracer avec soin C' et la tangente T dans le repère orthonormal (o;i;j).
4)a)Déterminer trois réels a, b et c tels que la fonction F définie par F(x)=(ax²+bx+c)e-xsoit une primitive de la fonction f sur R
b) est un réel positif. Calculer en cm² l'aire, A(
est un réel positif. Calculer en cm² l'aire, A( ) du domaine compris entre l’axe des abscisses, la courbe C' est les droites d'équation x=0 et x=
) du domaine compris entre l’axe des abscisses, la courbe C' est les droites d'équation x=0 et x= .
.
pour la partie A, ça a été déja vu. pour la partie B, je n'y arrive pas.
* message déplacé >>> un exercice démarré dans un topic doit être poursuivi dans ce même topic, comme tu le sais déjà... *
Bonjour,
Partie A
a) quand la fonction monte, la tangente est positive.
Comme il n'y a que 2 possibilités, essayes-en une. Sinon, c'est l'autre.
b) le coefficient directeur de la tangente en un point est égal à la valeur de la dérivée en ce point.
Que vaut g'(0) ?
bonjour,
partie A c'est ok.
a) fonction g, courbe C et fonction g', courbe F.
b) coefficient directeur=1
Pour le a), il faut montrer que f0(x)+f'0(x)=2(x+1)e-x
Le b), c'est un grand classique sans trop de difficultés
Non, sinon tu trouverais des valeurs de x.
L'inconnue de l'équation différentielle, c'est y
y'+y=0 peut aussi s'écrire dy+ydx=0 d'où dy/y=-dx
Une primitive de dy/y est ln|y|
Une primitive de -dx est -x+C
donc on arrive à y=Ke-x
Bonjour,
Pour la question c) de la partie B, il faut montrer que (f0+u)'+(f0+u)=2(x-1)e-x
Ensuite, on prend u(x)=Ke-x pour déterminer f(x)
Pour la d), g(x) s'écrira comme f(x) à la question précédente, mais comme on connait précisément g(x) grâce à sa courbe, on peut déterminer K tel que g(0)=1
Pour la e), il faut écrire h'(x) en fonction de K, puis en déduire la valeur de K grâce à h'(0)=0
(f0+u)'+(f0+u) = f'0+u' + f0+u = f'0+f0+u'+u
Or u'+u = 0 d'après la question b), et f'0(x)+f0(x)=2(x+1)e-x d'après la question a).




