Inscription / Connexion Nouveau Sujet
Courbe Paramétrée
Bonjour, je n'arrive pas à faire un exercice 
, je n'ai jamais vu ceci dans mon cours :
On considère la courbe paramétrée :
x(t) = t2/2 + sin(t)
y(t) = ln(1-t)
a) Calculer l'équation de la tangente à la courbe en t = 0.
b) Déterminer la position de la courbe par rapport à la tangente au voisinage de t = 0. Préciser la nature du point (x(0), y(0)).
Merci.
Bonsoir,
1. M(x,y) appartient à la tangente à la courbe au point M(0) si, et seulement si, où Det est le déterminant.
2. Fais un développé limité de x(t) et y(t) lorsque t tend vers 0.
Si.
De toute manière, la nullité du déterminant ne fait que traduire la colinéarité des deux vecteurs...
Bref, il s'agit d'une droite donc son équation est du type ax+by+c=0. Tu détermines (a,b) en trouvant un vecteur normal (sachant que le vecteur vitesse est un vecteur normal) puis c en traduisant le fait que M(0) appartient a la droite.
C'est tellement plus direct avec le déterminant... Mais vu que ce n'est pas moi qui fait les calculs !
Supposons qu'il s'agit de
-----
1)
En t = 0:
x(0) = 0 et y(0) = 0
dx/dt = t + cos(t)
dy/dt = 1/(t-1)
dy/dx = (1/(t-1))/(t + cos(t)) = 1/[(t-1).(t+cos(t))]
(dy/dx)(0) = 1/(-1) = -1
Equation de la tangente en t = 0:
y = (x - xo).(dy/dx)(0) + yo
y = -x
-----
2)
DL au voisinage de 0 :
DL x(t) = t²/2 + (t - t³/6)
x(t) = t + t²/2 - t³/6
- x(t) = -t - t²/2 + t³/6
DL y(t) = -t - t²/2 - t³/3
y(courbe) - y(tangente) = -t - t²/2 - t³/3 - (-t - t²/2 + t³/6) = -t³/2
Or au voisinage de 0, x à le signe de t.
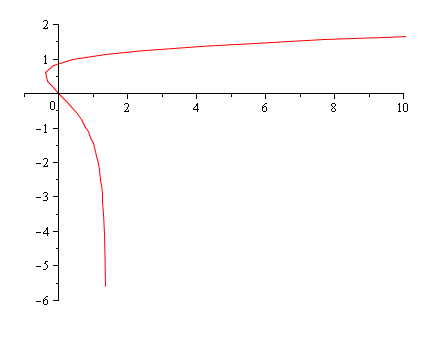
Donc la courbe est au dessus de sa tangente pour t < 0 (x < 0) (au voisinage de 0)
et la courbe est au dessous de sa tangente pour t > 0 (x > 0) (au voisinage de 0)
Le point (X(0) ; y(0)) est un point d'inflexion de la courbe.
-----
Sauf distraction ou erreur. Vérifie 
Annuler
connectez vous
analyse en post-bac