Inscription / Connexion Nouveau Sujet
Courbe paramétrée
Bonjour,
Je dois faire l'exercice suivant et j'ai quelques difficultés à comprendre.
Voici le sujet :
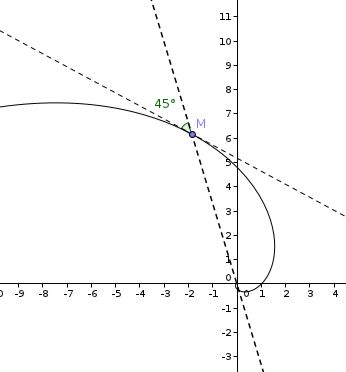
Le plan est rapporté à un repère orthonormal direct. Pour tout t, M(t) est le point de coordonnées x(t)=exp(t)*cos(t) ; y(t)=exp(t)*sin(t) et V(t) est le vecteur de coordonnées (x'(t), y'(t)). Je sais que pour tout t, le vecteur OM(t) est non nul.
Donc je dois faire le quotient de l'affixe de V(t) par celle de OM(t), et prendre son argument. Je sais que celui-ci est une valeur constante et je dois en déduire une propriété géométrique sur la courbe décrite par M(t).
Faire les calculs n'est pas un problème, mais je ne sais pas du tout de quelle propriété on parle. Pourriez-vous m'en dire un peu plus s'il vous plait ?
Merci d'avance !
Merci pour les calculs c'est gentil mais je les avais déjà !
En fait, je ne comprends pas la méthode, ni ce que cela apporte de savoir que l'angle est constant pour la courbe... ??
je dois en déduire une propriété géométrique sur la courbe décrite par M(t).
Mais l' angle entre

manifestement, le caractère particulier de cette relation constante entre un rayon et une tangente n'affole pas les foules.
Peut-être qu'avec
des élèves de Terminale un peu habitués aux beautés des Mathématiques, même élémentaires

Que disait Déproges, déjà, à la question de savoir si on pouvait faire de l'humour à propos de tout ?
Mais que serait l'existence sans humour ? 
(je concède le droit à chacun de trouver le mien un peu lourd...)
Certes il s'agit bien d'une propriété géométrique, mais cela sert à quoi d'avoir ça ?
En fait, les calculs ne sont pas le problèmes, mais je ne comprends pas pourquoi on fait le quotient des arguments, ni à quoi sert ''concrètement'' cette propriété... ?
Les maths n'ont strictement aucune utilité
sauf peut-être t'apprendre à réfléchir (j'oserai dire conceptualiser, mais j'ai peur que le mot ne te fasse fuir)
ah, dernière chose : sans les maths, pas d'internet, pas de téléphone, pas de trains, pas de moteurs, rien, quoi
à part ça, les maths ne servent à rien.
maintenant, savoir que l'angle de cette spirale logarithmique est constant ne te servira jamais à rien à toi, j'en fait le pari.
cet exercice est seulement là pour t'entraîner à manipuler les concepts (encore un mot horrible) qui te sont présentés dans le cours, ici les nombres complexes.
on fait le quotient des arguments,
non, on a calculé l'argument du quotient
et cet argument est justement une mesure de l'angle entre les deux vecteurs dont les affixes sont les complexes dont on t'a demandé de faire le rapport.
Revois ton cours.
Dis donc pas besoin d'être désagréable.
Si tu ne veux pas aider, ne poste pas.
Je ne demande pas à quoi servent les maths, je demande à quoi peut bien servir d'avoir l'angle entre la courbe et le vecteur directeur. Les mathématiques ont TOUJOURS pour but de répondre à un besoin, et je ne pense pas ici que l'on calcule cet angle pour le plaisir.
Ensuite, j'ai confondu les mots arguments et affixes. Cela arrive, désolée.
Dis donc pas besoin d'être désagréable
faudrait pas prendre tes désirs pour la réalité
où as-tu vu que j'étais désagréable ?
d'abord j'estime que tu ne me connais pas assez pour être aussi affirmative.
ce n'est pas de mon fait si tu démarres au jugé sur une expression qui a eu le malheur de te déplaire.
si tu souhaites que je sois vraiment désagréable, préviens-moi, je me ferai un plaisir de t'assouvir.



 analyse en Bts
analyse en Bts