Inscription / Connexion Nouveau Sujet
Courbe paramétrée
bonjour
svp je veux savoir les branches infinie de γ(t):{f(t)=1/(1-t*t) et g(t)=1/(1-t)(t*t+2t+2)}
Et je savoir la définition TANGENTE DE PENTE ????' les courbes paramétrée' et merci d'avance 
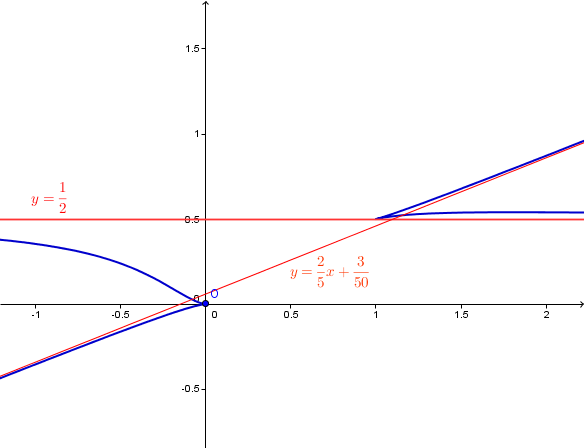
slt cailloux mrc mais j'ai un petit soucis sur la limite en + et - inf .. c'est 0 oui mé je ne sais pas pourquoi le prof nous a dit que ' la branche se prolonge en (0;0) avec une tangente de pente et il a calculer la lim quand t t'envers l'inf de (g(t)-g(0))/(f(t)-f(0))=0 il a dit cé une tangente horizontale . svp j'ai pa compri se truc mrc d'avance
L' origine du repère n' appartient pas à la courbe. Mais pour le dessin, on "prolonge" cette courbe par ce point
D' autre part, le coefficient directeur d' une tangente au point à une courbe représentative d' une fontion
est donné par
Le coefficient directeur ou pente de la tangente à l' origine est donné ici par
j'ai pa bien compris efff pourquoi tangente horizontale !! svp est ce que tu peux me donner les regles que je dois connetre pour savoir est ce que cé t'une TANGENTE HORIZONTALE OU BIEN VERTICALE ..
' si lim vers l'inf de (g(t)-g(0))/(f(t)-f(0))=0 tangente horizontale et si par exemple on a trouvé la limite égale l'inf !!! ' mrc
Voyons:
Si le coefficient directeur (ou la pente) de la tangente est nul, cette tangente est horizontale.
S' il tend vers l' infini, elle est verticale.
De rien aminasmile.
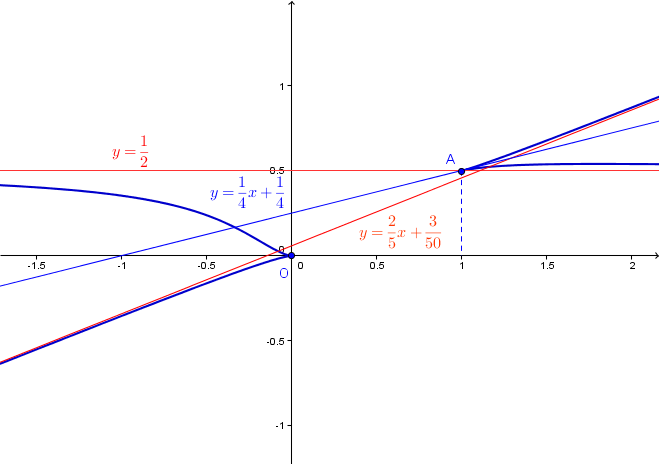
Pour information, ta courbe présente aussi un point de rebroussement de première espèce en pour
et l' équation de la tangente en ce point est
oui le points de rebroussement est dérigée par un vecteur U(4;1) svp je veux savoir comment tracer U
ET MRC BCP CAILLOUX
On travaille au voisinage du point singulier de paramètre
L' équation de la tangente est de la forme:
On calcule:
Puis l' équation de la tangente au point d' abscisse 1:
avec
,
et
qui donne
Annuler
connectez vous
analyse en post-bac