Inscription / Connexion Nouveau Sujet
Courbe Planes Paramétrées.
Salut,
J'aimerais bien que vous m'aidiez à résoudre cet exo 
J'y ai essayé biensur. J'espère que ce que j'ai fait est correcte.
Je me coince dans la représentation graphique.
L'énoncé:
On a une courbe définie par:
x(t)=(t²+1).e-t²/2
y(t)=t.e-t²/2
Représenter la courbe.
Ce que j'ai fait:
x'(t)=t(1-t²).e-t²/2
y'(t)(1-t²).e-t²/2
| t | -oo ____ -1 | -1 ____ 0 | 0 ____ 1 | 1 ____ +oo | |
| x'(t) | + | - | + | - | |
| y'(t) | - | + | + | - | |
| x(t) | 0-->2.e-1/2 ( croissante) | 2.e-1/2-->1 (décroissante) | 1-->2.e-1/2 (croiss.) | 2.e-1/2-->0 (décroiss.) | |
| y(t) | 0-->-e-1/2 ( décroiss.) | -e-1/2-->0 (croiss.) | 0-->e-1/2 (croiss.) | e-1/2-->0 (décroiss.) |
Les valeur selon t ( les points intéressants).
| x | y | x' | y' | x'' | y'' | x(3) | y(3) | |
| t=-1 | 2.e-1/2 | -e-1/2 | 0 | 0 | -2.e[sup]-1/2 | 2.e-1/2 | 2.e-1/2 | 2.e-1/2 |
| t=0 | 1 | 0 | 0 | 1 | 1 | 0 | 2.e-1/2 | 2.e-1/2 |
| t=1 | 2.e-1/2 | e-1/2 | 0 | 0 | -2.e-1/2 | -2.e-1/2 | -2.e-1/2 | 2.e-1/2 |
M(t=1,-1)des points stationnaires.
x"(t)=(t4-4t²+1).e-t²/2
y"(t)=(t3-3t)
x(3)(t)=(-t5+8t3-9t).e-t²/2
y(3)(t)=(-t4+6t²-3).e-t²/2
Pour,
* M-1(2.e-1/2,-e-1/2)
Det[(x",y"),(x(3),y(3))]
0
rebroussement de la 1ère espèce.
* M0(1,0)
Det[(x',y'),(x",y")]
0
point de concavité
*M1(2.e-1/2,e-1/2)
Det[(x",y"),(x(3),y(3))]
0
point de rebroussement de la 1ère espèce.
Voilà.
Mais comment présenter tout ce calcul, s'il est correcte tout d'abord,...?
Merci infiniment!
Bonjour
Tout ça a l'air juste et c'est comme ça que l'on présente!
Voici un tracé (informatique) qui te permet de vérifier les détails.
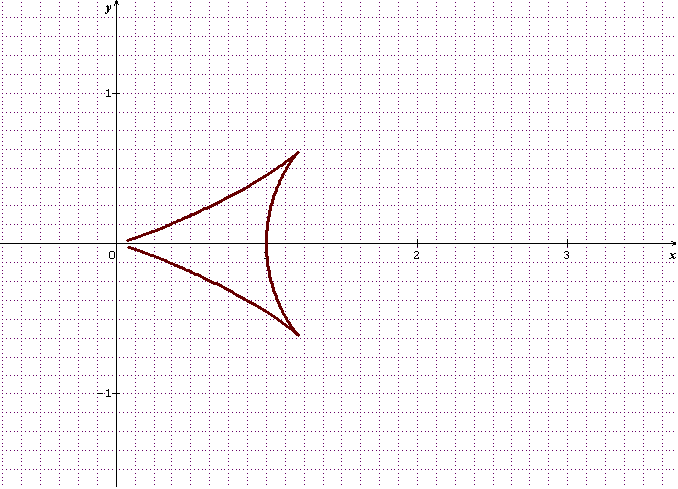
Ben, tu suis à la trace... Pour t entre " alt="-
" class="tex" /> et -1, x(t) croit de vers
et y(t) décroit de
vers
. la courbe se déplace donc à partir de (0,0) vers la droite (x croit) et vers le bas (y décroit) jusqu'au point
(c'est la branche basse du dessin. Ce point est un rebroussement, ensuite on change de sens...
La tangente en un point de rebroussement est le premier vecteur dérivé non nul. Ici, par exemple c'est
Annuler
connectez vous
analyse en post-bac