Bonsoir

C'est les fonctions hyperboliques ou non ?

C'est la formule de Moivre.

oui c'est bien les fonctions hyperboliques

et je ne connais pas Moivre désolé

tu pourrais juste me dire comment développer cette formule pour pouvoir arriver a la bonne réponse?

bonjour,

après avoir vu la formule de Moivre sur internet et sa démonstration, j'ai vu qu'elle mettait en relation avec des nombres complexes, chose que je n'ai pas encore vu.

puis je appliquer la démonstration sans utiliser le "i"?

peut-être par récurrence ?

as-tu lea démonstration par récurrence en cours ?

oui je les ai mais je ne savais pas si ca marchait également si on enlevait le "i"

pour ne pas que je me trompe, la démonstration par récurrence ici est bien:





peut on faire ca en enlevant les "i"?

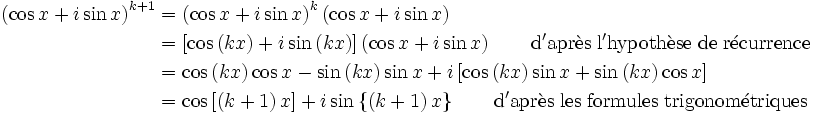
non, sans partir de la formule de Moivre mais de la tienne :

(cosh (x) + sh (x))^n = cosh(nx) + sh(nx)

mais alors cela ne marcherais que pour n>0

pour n = 0 cela ne pose pas de problème

mais pour n<0???

puis je appliquer ceci?
si n = -m

généralement, les formules en ^n ne sont à considérer que pour n entier supérieur ou égal à zéro

tu tiens absolument à prendre la formule avec i alors que tu ne l'as pas vue en cours ?

ok ca va

un grand merci