Inscription / Connexion Nouveau Sujet
demonstration formule de Cardan
Bonjour a tous,
Je dois démontrer la formule de Cardan qui est attachée dans le cas x^3=px+q
J'ai eu un exercice avant cette question avec x^3=3x+14
et j'ai un systeme que voici : u^3+v^3=14
uv=1
Merci de bien vouloir m'aider 
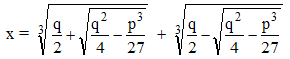
Un axe à suivre sans rigueur : Posons et
. Ainsi a-t-on
. Imposant
, i.e.
, alors
. Tout revient (sic) à résoudre le système
, équivalent au système
. L'on constate donc que
et
sont solutions de l'équation
, avec
.
A +
Un axe à suivre sans rigueur : Posons et
. Ainsi a-t-on
. Imposant
, i.e.
, alors
. Tout revient (sic) à résoudre le système
, équivalent dans
au système
. L'on constate donc que
et
sont solutions de l'équation
, avec
. Supposant
(à préciser en fonction de ton énoncé !), l'on trouve
et
, voire
et
, de sorte qu'au final
.
A +
je viens de le refaire et je ne comprend pas comment vous obtenez le u^3+v^3+(u+v)(3uv-p)-q
Car j'obtiens u^3+v^3-p(u+v)-q
Je ne le sais pas, mais je me suis arrangé pour écrire les choses de la sorte en fonction de la réponse à donner. Cependant, en considérant l'équation , tu peux aussi remarquer que
. Tu vas retomber sur les solutions tant attendues !!
A +

 (q/2)
(q/2) :D
:D

