Inscription / Connexion Nouveau Sujet
Démonstration l'air d'une sphère
Salut
J'ai une question concernant à la démonstration du l'air d'une sphère , j'ai pas compris pourquoi =4πr^2 et r c'est le rayon du sphère, j'ai essayé de faire une démonstration par intégration : je prend un petit élément du surface ( dx , dy) tel que
Les bornes d'intégration sera
C'est la surface d'une demi sphère donc il faut que multiplier par 2 donc ça sera 2*π^2*r^2 je n'arrive pas à comprendre ou j'ai trompée ,
Merci
Bonjour, les côtés de ton élément de surface, dx et dy, ne sont pas bons.
Il y a des sin et/ou sin
et/ou sin (ou cos) qui trainent là dedans. Non?
(ou cos) qui trainent là dedans. Non?
heu non les angles ne sont pas indépendants
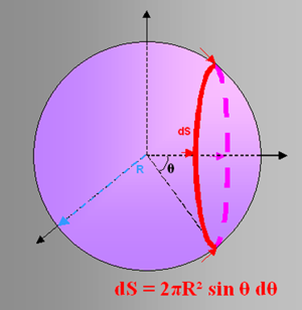
le plus simple est d'intégrer sur des couronnes
le cercle a un rayon r = R sin  donc une circonférence 2
donc une circonférence 2 R sin
R sin  et l'élément d'aire est donc 2
et l'élément d'aire est donc 2 R sin
R sin  (R d
(R d )
)
tu intègres ça entre 0 et 
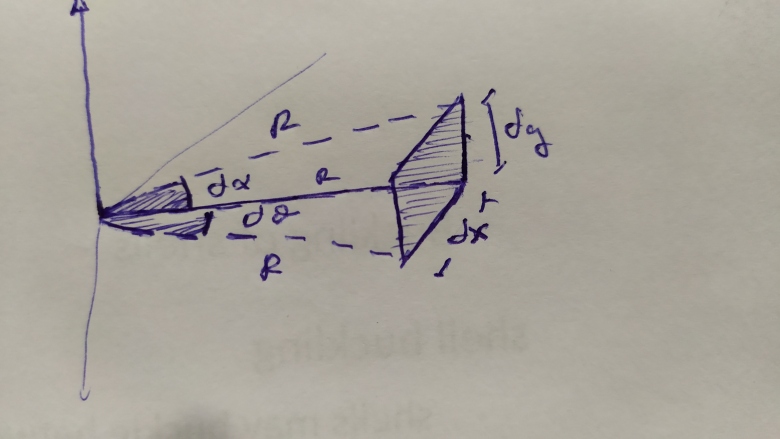
Merci pour les réponses , jusqu'à maintenant je n'arrive pas à comprendre pour quoi les angles ne sont pas indépendants par exp : je vais choisir deux angles et dx =R*d et dy=R*d
et dy=R*d dx et dy ce sont des petites segment dx et dy ne dépant pas on x ou y .
dx et dy ce sont des petites segment dx et dy ne dépant pas on x ou y .


 analyse en post-bac
analyse en post-bac