Voilà un exercice que je ne parviens pas à résoudre, merci d'avance pour vos réponses

1) dans un plan d'un muni d'un repère orthonormé (O, , ) on considère de cercle , de centre O et de rayon 1.
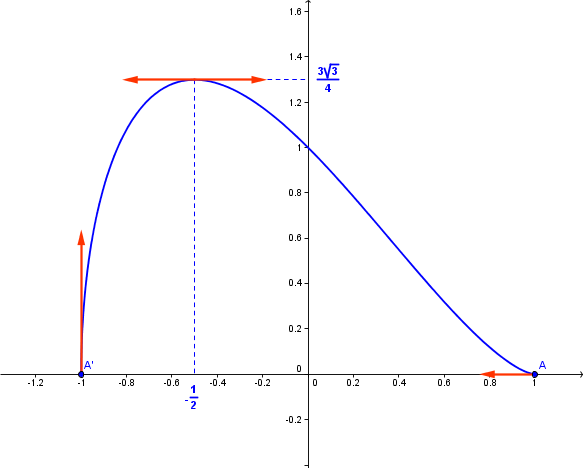
Soit A le point de coordonnées (1;0) et A' le point de coordonnées (-1;0).
Par tout H du segment [AA'], distinct de A et de A', on mène la perpendiculaire a la droite (AA').
coupe le cercle en M et M'. On pose \vec{OH} =\vec{xi}

Calculer l'aire du triangle AMM' en fonction de x.

j'ai réussit cette question pour laquell j'ai trouvé : Aire =

2) Soite f la fonction definie par f(x) = (1-x)(1-x²)  

a)etudier la derivabilité de F aux point d'abcisse -1 et 1.
là j'ai trouvé f'(-1) et f'(1) = 0 donc deux tangentes horizontales a ces points là.

là ou je ne comprend pas c'est la question d'après :
on demande de faire le tableau de variation de f sur l'intevalle [-1;1].
pour cela notre prof nous avait dit de penser a deriver f.
j'ai donc considéré f comme une fonction composée de type f(x) = uv(g)

avec u = (1-x)
     v = (x)
     g = (1-x²)

je sais dériver ca, sauf que d'après ce qu'on a fait en cours, une fonction (u) que si u est derivable sur I et si elle est supérieure a Zero.
Or ici, dans ma fonction v(g); g n'est pas strictement supérieure a 0.

Ou alors je suis complètement a coté de la plaque ... ? ( c'est fort possible )

merci pour votre aide !