Bonsoir Nathalie-Marie;
tu commences par remarqer que ta fonction est définie pour et qu'elle est dérivable pour et puis tu écris en développant le :

tu dérives comme si tu as un exposant entier c'est à dire que:

tu vois bien maintenant que le signe de sur est celui de

Une erreur serait de séparer les facteurs du dénominateur et de simplifier par pour obtenir:

mais cette expression de n'est définie que sur alors que notre fonction est dérivable sur

J'ai une autre vision des choses mais qui n'engage que moi.

C'est une habitude maintenant de vouloir à tout prix définir une puissance à partir des logarithmes.
On en arrive à nier l'existence de solutions pour des racines cubiques de nombres négatifs.(la racine cubique de -8 est -2 (dans R))

Pour moi, le domaine d'existence de f(x) est R.

f(x) = (x³-3x+2)^(1/3)

f '(x) = (1/3).(x³-3x+2)^(-2/3).(3x²-3)

f '(x) = (x²-1)/(x³-3x+2)^(2/3)

f '(x) a le signe de x²-1, f'(x) existe sur R - {-2 ; 1}

f '(x) > 0 pour x dans [-oo ; -2[ --> f(x) croissante
f '(x) n'existe pas pour x = -2
f '(x) > 0 pour x dans ]-2 ; -1[ --> f(x) croissante
f '(x) = 0 pour x = -1
f '(x) < 0 pour x dans ]-1 ; 1[ --> f(x) décroissante
f '(x) n'existe pas pour x = 1
f '(x) > 0 pour x dans ]1 ; oo[ --> f(x) croissante

Il y a un max de f(x) pour x = -1
Il y a un point de rebroussement dans la courbe représentant f(x) pour x = 1

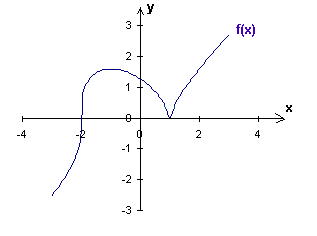
Sur le dessin uune représentation de f(x) limitée à l'intervalle [-3 ; 3] pour x.
-----
Sauf distraction.  

petite question rapide : qu'est-ce qu'un rebroussement ? merci

basso, pour en savoir plus , consulte par exemple les sites suivants: et

merci

J-P, il y a probablement un chouia plus simple pour connaître les variations de f.

Tu écris :
"f(x) = (x³-3x+2)^(1/3)
f '(x) = (1/3).(x³-3x+2)^(-2/3).(3x²-3)
f '(x) = (x²-1)/(x³-3x+2)^(2/3)
f '(x) a le signe de x²-1, f'(x) existe sur R - {-2 ; 1}
f '(x) > 0 pour x dans [-oo ; -2[ --> f(x) croissante
f '(x) n'existe pas pour x = -2
f '(x) > 0 pour x dans ]-2 ; -1[ --> f(x) croissante
f '(x) = 0 pour x = -1
f '(x) < 0 pour x dans ]-1 ; 1[ --> f(x) décroissante
f '(x) n'existe pas pour x = 1
f '(x) > 0 pour x dans ]1 ; oo[ --> f(x) croissante"

En fait, la fonction "racine cubique" est croissante, donc f a mêmes variations que x |-> x³-3x+2, dont l'étude est plus simple.

Nicolas

Je comprends votre vision J-P (Correcteur),mais réstreindre les puissances rationnelles(ou réelles en général)aux réels positifs est une convention adoptée pour permettre à celles-ci de vérifier toutes les propriétés des puissances entières telles que:


( )
avec, on aurait par exemple:
puisque le terme de droite n'a pas de sens dans ( ni dans )
c'est donc essentiellement dans un souci de compatibilité avec les régles de calcul sur les puissances .

Bonjour elhor_abdelali

Je comprends aussi la motivation de la restriction imposée que tu mentionnes, mais comme je ne suis pas mathématicien mais plutôt physicien, ces restrictions ne me plaisent pas.

Si lors d'une études d'un phénomène physique, on tombait sur un cas similaire d'équation, ignorer ce qui se passe dans la partie ]-oo ; -2[ de la courbe pourrait être fort préjudiciable à la compréhension complète du phénomène étudié.

Je suis de ceux qui pensent que les maths sont d'abord et avant tout un outil pour aider les physiciens et je tique alors systématiquement lorsqu'on néglige une partie existante d'un problème par seul soucis de pouvoir étendre une règle mathématique sur un plus grand domaine. (mais en ratant une partie pourtant bien existante du problème).
  
Mais je suis peut-être le seul, surtout sur un forum de maths à avoir cette opinion.

Bonjour J-P (Correcteur),pour ne pas ignorer ce qui se passe sur il suffit de considérer la fonction:
c'est le graphe de cette fonction que tu as représenté.