Inscription / Connexion Nouveau Sujet
dérivée
Bonjour,
Je souhaiterai réaliser la dérivée en un point d'une fonction.
Néanmoins, je ne connais pas la formule analytique de cette fonction, je ne dispose que:
-soit de valeurs tabulées de la variable et de la fonction
-soit d'un graphique où il y a la courbe représentative de la fonction
De ce fait, via quelques recherches, j'ai différentes approximations possibles:
f'(xi)
(yi+1-yi)/(xi+1-xi)
Ou encore
f'(xi)(yi+1-yi-1)/(xi+1-xi-1)
Laquelle est préférable ? Ou puis-je utiliser d'autres méthodes ?
Notamment via la méthode d'Euler ?
Merci d'avance
Bonjour,
Pour ce qui est de la comparaison, pour une fonction "normale", la deuxième est préférable (voir le dessin ci-dessous).
Pour ce qui est des autres méthodes voir : 
La méthode d'Euler, c'est votre première expression.
Bonjour
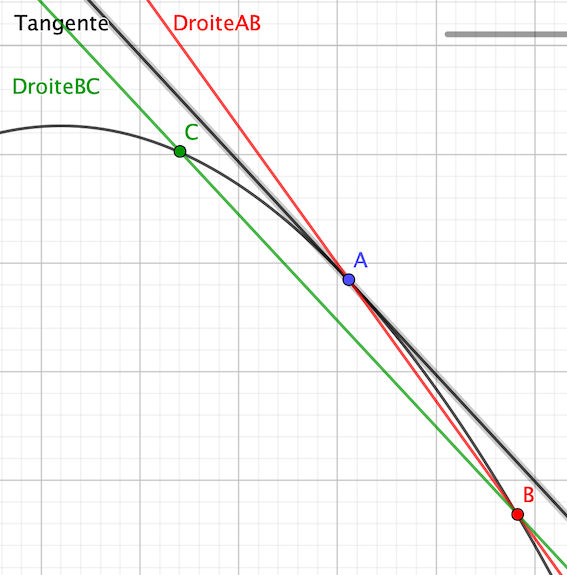
des tangentes figurent-elles sur le graphique ? avec quelle précision peut-on y faire des lectures ?
La tangente est en noire et il est indiqué en noir "Tangente".
Le schéma est là pour visualiser la différence entre les deux méthodes pas pour faire des lectures (même si, bien sûr, on peut le faire)
D'accord.
Même si la seconde méthode semble plus précise, je vais choisir la 1ère méthode pour être en accord avec le contexte.
Merci
Bonjour,
Quitte à enfoncer des portes ouvertes :
En toutes circonstances, une méthode d'approximation doit être accompagnée d'un majorant de l'erreur commise.
Comparer ces majorants, dans le but de déterminer quelle est la meilleure méthode, est une très mauvaise idée.
Je ne comprends pas bien la dernière phrase. Pourquoi cela serait une très mauvaise idée ?
Comparer ces majorants peut être un paramètre à prendre en compte pour le choix de la méthode à utiliser (comme aussi la simplicité du calcul)
Annuler
connectez vous