Inscription / Connexion Nouveau Sujet
dérivée fonction...
Bonjour,
Dans un exercice on me demande de montrer que f'(x) a le signe de g(x) sur ]1, +infini[. En déduire les variations de f(x) sur I. Montrer que f(a)=3a ( on pourra calculer f(a) - 3a )
Mes résultats sont :
g(x)=x3-3x-3 sur
f(x)= (2x3+3)/(x²-1) sur I=]1;+[
1) Étudier les variations de g(x)
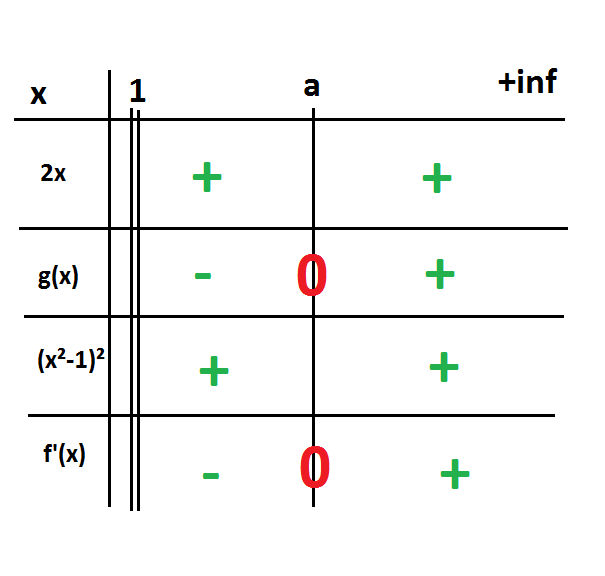
Donc j'ai fait le tableau de variation pas de problèmes
2)Démontrer que l'équation g(x)=0 admet une unique solution sur [1;3] que l'on note a. Donner un encadrement de a à 10-2 près et en déduire le signe de g(x).
Donc pas de problème non plus ici, j'ai trouvé 2,1<a<2,11 comme encadrement.
Et là arrive la question posée au dessus.
J'ai calculé la dérivée de f(x) et f'(x) = (2x4-6x²-6x)/(x²-1)²
On sait que sur ]1;+infini[ g est supérieur à 0.
De plus, (x² + 1)² est positif étant un carré et 2x est supérieur à 0 sur ]1 ; +infini[
on retrouve enfin g(x) dans le deuxième facteur de f'(x) et là je bloque...
Oui pardon 2x(x^3-3x-3) /(x²-1)² 
On sait que le dénominateur et 2x sont positifs sur ]1; +infini[ mais il reste g(x) ...
Oui mais le problème c'est que sur a est environ égal à 2.1 et g(a)=0 et g(x) est positif sur [a; +infini[ et pas sur ]1;+infini[ donc je ne sais pas comment faire :/
Donc sur [1;a], g(x) est négatif et sur [a;+infini[ g(x) est positif mais alors comment on sait le signe de g(x) sur cet intervalle ? ( désolé de ne pas comprendre)
Ah d'accord je comprends mieux avec le tableau 
Et après à partir du tableau de signe je fais le tableau de variation de f(x) croissant quand c'est le signe + et décroissant quand c'est le signe - comme ça :
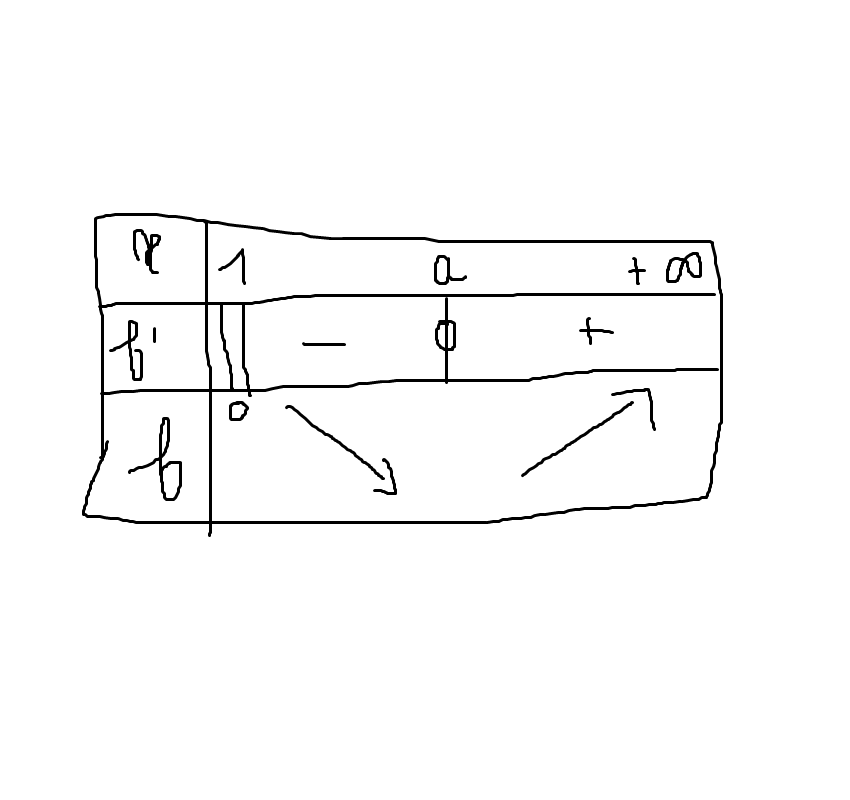
Je ne comprends pas comment fait-on pour passer de cette ligne de calcul :
f(a) = (6a + 9)/((3a +3 - a)/a) à celle-là (3a(2a+3))/(2a+3)