bonjour
as-tu commencé sachant que la première question est facile..

non , Et je comprend pas ma leçon dans mon cours ..

bon
allons y pas à pas

sais-tu dériver une fonction?

Pas du tout ..

voir Cours sur les dérivées et la dérivation

la partie II

puis voir les exercices corrigés après avoir essayé Quatre exercices d'applications pour débuter la dérivation

Donc ma première question c'est :
F(x)=x2+x-2
F'(x)=2x+1

voilà!

que peux-tu dire du signe de ta dérivée f'?

Elle est positif ?

tu es sûr(e)?
pour x=-3, f'(x)=-5

donc est-ce toujours positif?

Non pas toujours Mais Dans mon cas oui

bah x=-3 appartient pourtant à ton intervalle...

Mon intervalle c'est [-4;3]
Et je vois pas où mon  x Peut etre -3

résous 2x+10

2x+1>0
On remplace x par n'importe quelle chiffe donc par exemple 2x2+1 =5 donc c'est supérieur à 0

bah non...

tiens une représentation graphique de ta dérivée f' ...

et puis pour résoudre une inéquation on n'agit pas comme ça...

exemple:

3x+1>0
3x>-1
x> -1/3

donc 3x+1 est positif sur ]-1/3;+oo[

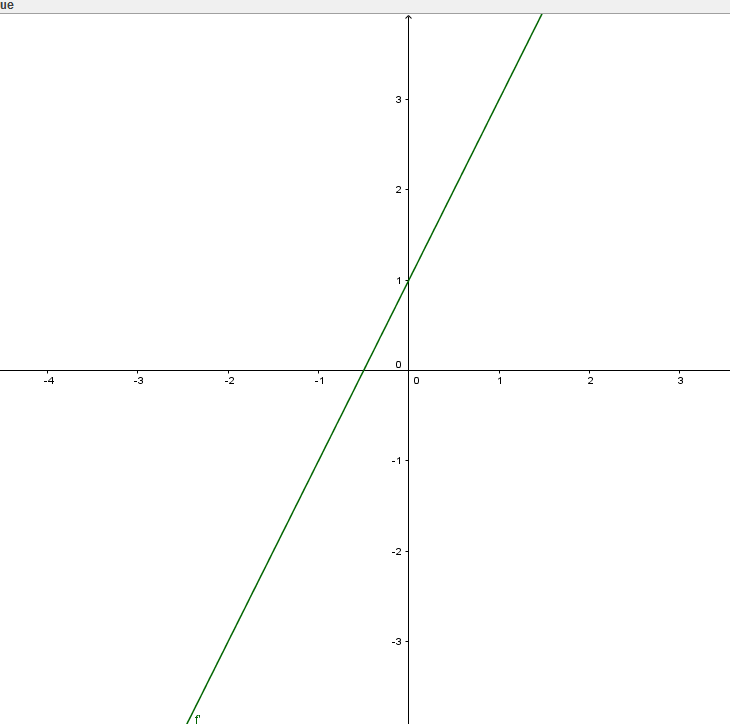
Donc si j'ai bien compris
Mon équation est :
2x+1>0
2x>-1
X>-1/2
Donc 2x+1 est positif Sur l'intervalle -1/3

aide toi de ma représentation graphique...
c'est plutôt sur l'intervalle ]-1/2;3]
et donc négatif sur ......

Je suis désolée je comprend plus la ..

Ah peut etre Que j'ai compris donc Elle est négatif en -Infini ; -1/2

tu es d'accord que c'est x>-1/2
donc c'est positif sur ]-1/2;+oo[ mais comme on est limité à x=3 d'où l'intervalle ]-1/2;3]

mais on est à x=-4 donc quel est l'intervalle?

C'est [-4;-1/2]

c'est ça

tu peux en faire un tableau de signe
pour faire le tableau de variations de f

Ah donc La Je fais mon tableau de variation ?

oui tu peux, en connaissant le signe de f'
si f' est positive, f est croissante
si f' négative, f décroissante

Je calcul comment une équation réduite de la tangente ??
Je suis désolée je vous prend tout votre temps Mais Avec vous je comprend petit a petit

avec l'expression
y=f'(a)(x-a)+f(a)

ici a=0
donc y=f'(0)*x+f(0)

Y=f'(0)x(x-0)+f(0)
On sait que f'(0) est égale a 0 donc y est égale 0 ( x-0) +f(0)
On sait que f(x)=x^2 donc f(0) est égale 0^2 = 0
D'où y=0( x-0)+0
Y=0x-0+0
Donc y est égale 0x

C'est ça ??

f'(0)=2*0+1=....
f(0)=0²+0-2=

f'(0)=2*0+1=1
C'est juste ?

oui
et pour f(0)?

C'est -2

Comment je montre que f(x) =(x+2)(x-1) ??

en seconde, tu aurais pu développer cette expression pour retomber sur celle que tu as dans l'énoncé mais ça m'étonnerait que ça soit cela que l'on attende de toi

as-tu déjà vu les calculs avec ?

Pas du tout ..
C'est peut etre une double distributivité ?

je sais que c'est une double distributivité
en développant cette expression, tu tombes sur la première expression, ça c'est sûr

si tu n'as pas vu le discriminant (b²-4ac) il n'y a pas d'autres manières que la distributivité

lire =b²-4ac

Je l'ai effectivement pas vu
Donc je fais une distributivité

oui

Pour la question 4b Et 4c c'este toi noir ... je comprend rien ...

C'est le trou noir *

tu parles peut-être des questions 5 et 6?

voir Exercice Equations et inéquations

Oui oui pardon

va voir l'exercice proposé

Pour la question 5 c'est
X+2=0
X=-2/1=-2

X-1=0
X=1
Vous pensez que ça à l'air bon ?

il faut juste rajouter "ou" entre les valeurs !

Aaah merci beaucoup
Pour la question 6 ?

la même démarche sauf qu'il faut faire attention au signe de l'inégalité
ça donne quoi alors?

Euh je suis perdu La