Inscription / Connexion Nouveau Sujet
Déterminant de Gram
Bonjour, j'ai besoin dans cette question.
Soit E un espace vectoriel euclidien de dimension p sur R (p ≥ 2). Pour (x1,...,xn) donné dans E^n, on pose G(x1,...,xn) = (xi|xj)1≤i,j≤n
Montrer que rg(G(x1,...,xn)) = rg(x1,...,xn).
Bonjour soufianelh.
Les vecteurs colonnes de la matrice de Gram admettent les mêmes relations de dépendance linéaire (dans l'espace des n-uplets de réels) que les vecteurs
dans E : si on note
la famille des vecteurs colonnes de la matrice de Gram, on a pour toute famille de réels
si et seulement si
Il s'ensuit que la famille de vecteurs et sa matrice de Gram ont le même rang.
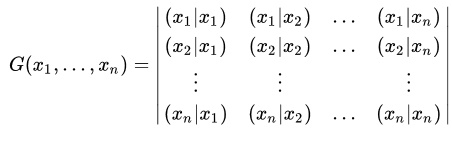

 sauf erreur bien entendu
sauf erreur bien entendu
 algèbre en post-bac
algèbre en post-bac