Bonsoir,

f n'est pas dérivable en 1 (la tangente à la courbe est verticale). Mais f" change de signe en 1.

Je suis désolée, je ne comprends toujours pas :s
Les points d'inflexions sont bien les points où la dérivée seconde s'annule en changeant de signe.
Si f'' ne s'annule jamais, comme puis-je conclure à un point d'inflexion, quand bien même f'' change de signe en x=1, ce n'est pas une condition suffisante ?

Ton calcul a dû tout de même te convaincre que f" est > 0 pour x <1 et <0 pour x > 1, non ? Bien sûr f" ne s'annule pas en 1 puisque la fonction n'est pas dérivable en 1. Mais on peut aussi changer de signe en pasant par l'infini. Un petit desin t'aidera peut-être à comprendre.

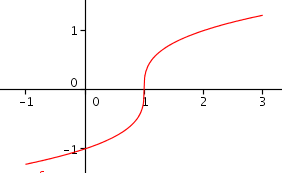
Si je comprends bien, quand une fonction f n'est pas dérivable en un point mais que f'' change de signe en ce point, on peut conclure que la fonction admet un point d'inflexion ?

Il faut voir en quel sens on parle de point d'inflexion.

Une approche raisonnable ici serait de parler de point d'inflexion au sens des courbes paramétrées planes. On a la paramétrisation y = t, x= 1+t³. En t=0 (correspondant au point (0,1)) on a x'y"-x"y'=-6t qui s'annule en changeant de signe, ce qui veut dire qu'on a bien un point d'inflexion de la courbe.