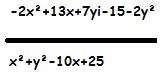Inscription / Connexion Nouveau Sujet
Déterminer Re(Z) et Im(Z) en fonction de x et y
Bonsoir, je suis en terminale S et je bloque sur l'exercice suivant:
Soit z un nombre complexe différent de 6 et Z = (2z-3)/(5-z).
On pose x = Re(z) et y = Im(z).
1. Déterminer Re(Z) et Im(Z) en fonction de x et y.
J'ai donc remplacé z par x+iy dans Z ;
Z= (2x + 2iy - 3 ) / (5 - x - iy)
Z= [(2x-3) + i2y] / (5-x) - iy ]
Et ici, je bloque. Si je multiplie par le conjugué je me retrouve avec des carrées et je suis perdue :/
Salut,
C'est jusute, continue avec le conjugué, tu vas finir sur cette forme (2x²-y-3a)/[5-(a²+b²)]+i(3ab-3b)[5-(a²+b²)].
Bonsoir !
J'ai le même exercice à faire sauf que z doit être différent de 5 et non de 6...
J'ai fait ce que vous avez dit et je tombe sur une très longue équation que je n'arrive pas à résoudre...
(j'ai fait un dessin sous paint, pour que ce soit plus clair)
Pourriez vous m'expliquer s'il vous plaît? Je patauge déjà beaucoup en cours ce moment donc j'aimerais beaucoup comprendre.
Ensuite on nous demande d'en déduire les valeurs de z pour que Z soit un réel:
en cherchant la réponse à la première question je pense que j'ai trouvé celle à la deuxième...
J'ai multiplié le numérateur et le dénominateur par le conjuguée du dénominateur puis j'ai calculé les racines du polynôme que j'ai trouvé au numérateur, et j'ai obtenu -5 & 1,5.
Cela vous semble-t-il juste?
Merci d'avance pour votre aide