Inscription / Connexion Nouveau Sujet
Developpement limité ( et post d hier si possible )
Bonjour
j'ai cette fonction ( pas trop méchante)
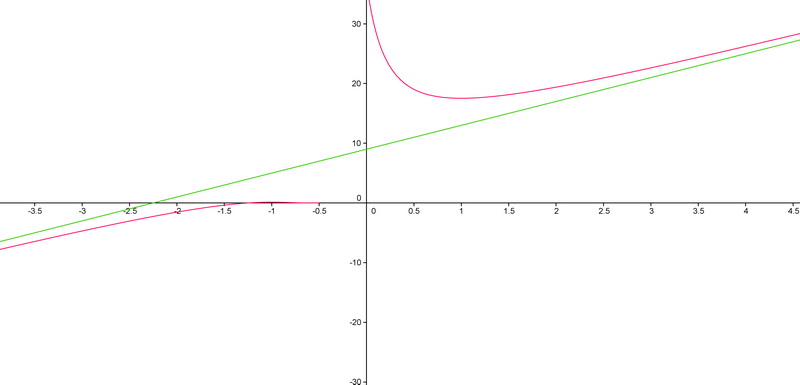
(4*x+5)*exp(2/(2*x+1)) Il y aurait une asymptote oblique à détecter
On nous donne l indication : poser t=1/x et donner leur position respective ( asymptote et courbe .je décroche içi
Merçi pour vos réponse
PS) a mon post d hier je n ai pas eu de réponse satisfaisante et pour éviter les multiposte ( j ai été exclu à cause de ça ) Pourriez vous y " jeter un oeuil
Merçi par avance
Diplo-docus
Bonjour à tous,
euh non Hiphigénie, ce n'est pas correct: lorsque tend vers
, le deuxième facteur (celui avec l'exponentielle) tend vers
!

et le 1er facteur tend vers + ...
...
Donc, la conclusion à tirer est que , mais cela ne renseigne pas l'existence d'une asymptote oblique.
Ouh là en effet, j'ai honte! 
De plus, un DL montre que tu as raison! J'ai inconsciemment ajouté les équivalents... 
Désolé Hiphigénie, j'ai parlé trop vite!
J'ai inconsciemment ajouté les équivalents
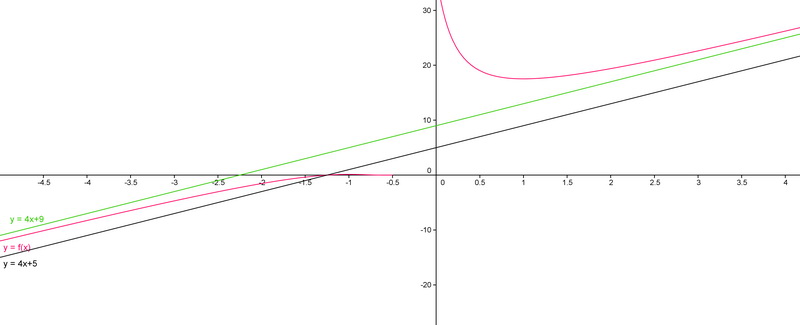
Enfin non, ce n'est même pas ça! 4x+5 est bien un équivalent de la fonction en l'infini, mais ce n'est pas pour autant que la droite y=4x+5 est asymptote obloque à la courbe en l'infini...Je suis mal réveillé, moi, on dirait...!
J'avoue que c'était tentant d'y croire, mais c'est comme pour le Père Noël, la réalité n'est pas toujours celle que l'on croit 
En outre, je ne vous pas en quoi un DL nous serait utile  ?... au voisinage de quel point ?
?... au voisinage de quel point ?
Il suffit simplement d'appliquer la définition d'une AO d'équation y = ax + b.
et
en utilisant le changement de variable :
.
idem en .
On peut en effet faire ainsi, mais ce n'est pas une définition, plutôt un théorème (certes assez élémentaire) que tu utilises.
Il me semble ici plus approprié d'utiliser un DL de l'exponentielle en , en posant
, avec




 analyse en post-bac
analyse en post-bac