Bonjour ambre1406
bon début

2) quand C' est-elle minimale (parabole, etc...) Fonction polynôme de degré 2 et parabole
vois-tu ?

Merci pour votre aide, j'ai donc utiliser la méthode que vous m'avez partagé:

C_m(x)= C'(x)= 3x²-60x+309
C'(x) et du type ax²+bx+c avec a= 3 b=-60 et c= 309

= -b/2a= 60/6=10
= f()
f()= 3x10²-60x10+309
f()=9
Donc =9

C'(x) est un polynôme du second degré dont la courbe représentative est une parabole a=3; a>0, la parabole est donc décroissante puis croissante (tournée vers le haut)

J'ai ensuite réalisé un tableau de variation de ma fonction ma parabole a donc pour minimum =9 atteint pour x=10 cela veut donc dire que le coût marginal est minimal pour 10paires de bottes fabriquées.

Est-juste ?
Merci

certes...mais bon, cela t'a fait une bonne révision ! mais....ce que tu as rédigé est inutile

sous cette forme C'(x)= 3 (x-10)²+9 c'est immédiat ! pour x=10, le carré vaut 0 et la valeur atteinte vaut 9
oui ?
(quand tu enchaînes des questions, demande toi pourquoi on t'a fait faire la question 1 avant la question 2 etc )
OK ?

D'accord merci je vais faire comme cela, par contre je ne comprends pas la partie B, je ne sais pas comment procéder pour  démontrer que le bénéfice vaut cette valeur, pouvez vous m'aider à trouver le bon raisonnement ?

la question à te poser, c'est comment calculer le bénéfice
bénéfice = ce que ça rapporte - ce que ça coûte

x paires de bottes rapportent...
le coût de fabrication de x paires de bottes est...
d'où le bénéfice

tu essaies...

coucou ..._{je mets un message car je trouve pas comment enregistrer ce post sur mes favoris et je trouve l'exo intéressant}

bonjour ciocciu
regarde cette image, tout en bas à gauche de la page

ah oui ...merci

Je pense avoir compris merci, x paires de bottes rapportent 201€ et le coût de fabrication de x paires de bottes est C(x)= x³-30x²+309x+500

Le bénéfice est donc ce que ça rapporte moins que ce ça coûte donc:
B(x)= 201x- C(x)
B(x)= 201x - (x³-30x²+309x+500)
B(x)= 201x -x³+30x²-309x-500
B(x)= -x²+30x² -108x-500

c'est bien cela (attention erreur de recopie à la dernière ligne)
tu continues maintenant ....tu vois comment ?

Oui en effet merci j'ai fais une erreur de recopie au niveau de mes puissances,  pour la dernière question je pensais utiliser un tableau de variations à partir de la dérivée de ma fonction B(x)  (en cherchant et )mais je ne sais pas si c'est ce qu'il faut faire

_{oui c'est ce qu'il faut faire ...}   

D'accord merci, je l'ai fais et j'obtiens pour dérivée de B(x)= -x³+30x²-108x-500
B'(x)= -3x²+60x-108

a=-3 ; b=60 ; c=-108
= -b/2a
=-60/-6= 10
=f()
donc f()= -3x10²+60x10-108
f()=-300+600-108=192
On a donc = 10 et =192


a=-3<0 donc la parabole est croissante puis décroissante et à partir de mon tableau de variation j'ai pu déterminer un maximum de 192 atteint pour x=10

J'en conclue donc que pour avoir un bénéfice maximum il faut fabriquer 10 paires de bottes et que la valeur du bénéfice maximum est de 192€

Est-ce correct ?

à vue de nez tout ça me semble parfait  ....

Super alors merci beaucoup pour votre aide

reBonjour à vous deux...
ciocciu ne devait pas avoir les yeux en face des trous

c'est le signe de la dérivée qui est intéressant, et non son max ou son min !!
un petit coup de geogebra nous confirme tout ça


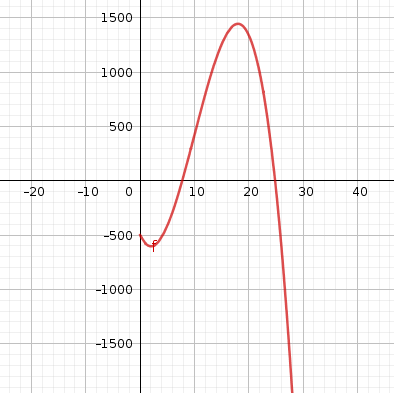
au boulot ! bénéfice maxi normalement atteint pour x=18 à démontrer proprement

D'accord, j'ai essayé de factoriser ma dérivée et j'obtiens:
B'(x)= -3x²+60x-108
B'(x)= -3(x² -20x+36)
B'(x)=-3(x²-2x-18x+36)
B'(x)= -3(x(x-2) -18x+36)
B'(x)= -3(x(x-2)-18(x-2)
B'(x)=-3 (x-2) (x-18)
Est-ce que cela peut me servir pour étudier le signe de la dérivée ? Si oui comment je dois procéder ?

OK, TB
signe de ton produit maintenant (tableau de signes par exemple, ou utilisation du signe d'un polynôme du second degré dont tu connais les solutions)

Alors j'ai fais mon tableau de signe mais je ne sais pas comment l'utiliser pour répondre à la question, et pour le signe du polynôme, comment est-ce que je dois procéder ?

ce polynôme (la dérivée) s'annule pour 2 et 18
le coefficient de x² est -3 (négatif)
donc ton polynôme est négatif partout sauf entre tes racines où il sera positif
revois cette fiche 4-Résumé sur les polynômes du second degré (la ligne signe de P(x) sur la fiche)

tu vois maintenant ?

D'accord merci mais alors cela veut dire que le bénéfice sera maximal seulement entre 2 et 18 (non inclus), puisque le signe de B'(x) est positif entre 2 et 18 ?

tu confonds bénéfice positif ou bénéfice maxi
le bénéfice maximum, c'est que ta fonction bénéfice admet un maximum
tu dois faire un tableau de variations pour la fonction bénéfice
x entre 0 et 30
signe de la dérivée
variations de B
maximum en fonction de ton tableau de variations
à toi

oula oui j'ai tout mélangé
merci malou _{c'est ça de faire des maths quand on travaille}