Inscription / Connexion Nouveau Sujet
DM 2nde
Bonjour alors voila je suis bloqué à la question 5 de l'exercice, je vous met tous pour que vous puissiez comprendre le contexte.
Une entreprise fabrique des pièces détachées pour automobiles.
On note x le nombre de pièces fabriqués au cours de la journée . Le coût de production, en centaines d'euros, de x est noté C(x)
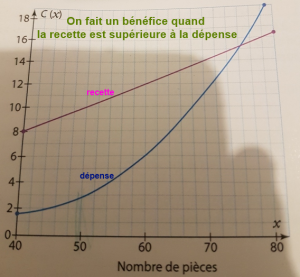
On a représenté en bleu la courbe de la fonction C. (Ci-joint)
À l'aide du graphique, répondre au questions suivantes:
1) quel est le coût de production de 50 pièces?
2) pour un coût de production de 1400 euros, combien de pièces l'entreprise va-t-elle fabriquer ?
On suppose que, sur l'intervalle [40;80], la fonction C est définie par C(x)=0.01x^2-0.79x+17.40.
3) chaque pièce est vendu 20 € déterminer la recette R(x),en centaines d'euros, de l'entreprise pour x pièces fabriquées.
4) vérifier que la droite tracer en violet et bien la représentation graphique de la fonction R
5) le bénéfice réalisé par l'entreprise en fonction du nombre x de pièce vendu est la différence entre la recette et le coût de production
Quel nombre de pièces entreprise doit-elle fabriquer et vendre pour réaliser un bénéfice positif?
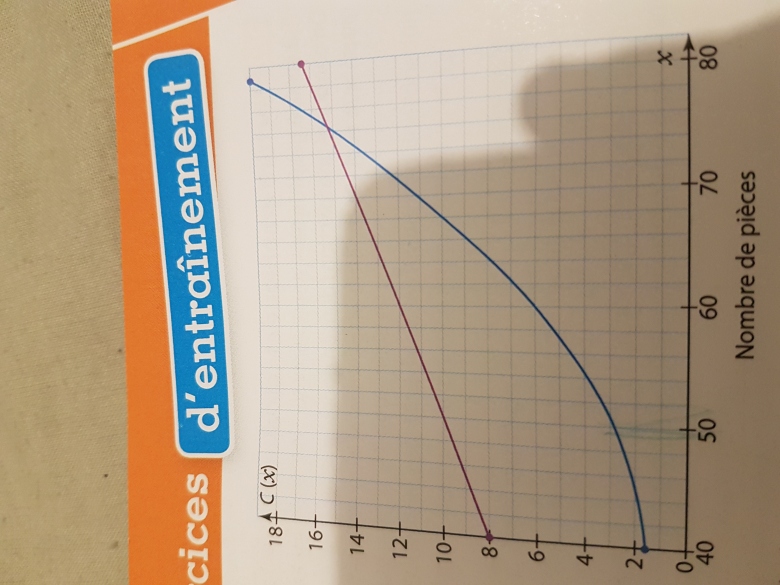
DSL pour l'attente donc alors
Pour faire du bénéfice (graphiquement) ils doivent vendre 76 pièces détaché au minimum
Est ce bien ça ?
Pour la recherche algébrique, continue comme te l'a demandé Yzz (bon exercice de calcul  )
)
B(x)=20x-(0,01x^2-0,79x+17,40)
Cette expression peut-être réduite en regroupant les termes en x...
Attention en supprimant la parenthèse....
Ok merci je vais essayer, je vous tiens au courant si j'y arrive ou pas
Merci à vous deux pour votre aide
Meilleurs voeux pour 2020
Merci pour tes voeux....
Mais il y a un petit problème 
La recette en euros est bien 20x mais on te la demande en centaines d'euros....
J'avais fait la même erreur mais quand j'ai essayé de représenter dans un même repère, les fonctions Recette et Coût..... l'évidence m'est apparue !!
Et si vous pouviez m'aider à isoler x, ça m'aiderai bcp car je n'y arrive pas malgré de nombreux essais...
Donc grâce à ZEDMAT , on est arrivés à :
B(x)=0,2x-(0,01x^2-0,79x+17,40) .
Tu as fait quoi ensuite ?
si vous pouviez m'aider à isoler x
Si "isoler x" c'est pour toi, trouver la valeur de x, alors là ça va être "compliqué"

Dans l'expression du bénéfice en fonction de x
B(x)=0,2x-(0,01x^2-0,79x+17,40)
tu peux supprimer la parenthèse (attention elle est précédée d'un signe "moins") et réduire.... c'est à dire regrouper les termes de même degré.
Essaye de faire cela. Tu vas voir que B(x) est un polynôme du second degré (c'est à dire de la forme ax²+bx+c).
C'est après que cela se "complique" !! si tu es bien en classe de Seconde....
On en reparlera demain si tu veux bien

Bonne nuit.
Oui je suis bien en seconde mais je n'ai pas encore travaillé sur ça 
Et je ne comprends pas 
Aidez moi svp
Et DSL pour le temps d'attente c juste que a cause des fêtes je n'ai pas vraiment eu le temps de me connecté
Enlever les parenthèses et réduire B(x)=0,2x-(0,01x²-0,79x+17,40) , c'est fait dès le collège !
A toi...
Dans l'expression du bénéfice en fonction de x
B(x)=0,2x-(0,01x^2-0,79x+17,40)
tu peux supprimer la parenthèse (attention elle est précédée d'un signe "moins") et réduire.... c'est à dire regrouper les termes de même degré.
Essaye de faire cela. Tu vas voir que B(x) est un polynôme du second degré (c'est à dire de la forme ax²+bx+c).
Ce que je t'avais demandé (ci dessus) est du niveau .... 3ème : réduire une expression algébrique. Essaye de faire....
Quand je le tape sur ma calculatrice, je remarque que pour faire du bénéfice , il faut que l'entreprise doit vendre au maximum 76pièces
Est ce bien cela?
Oui c bon je me souviens... trou de mémoire..
Donc on a
0.2x-0.01x^2+0.79x-17.4
2 conseils (ou consignes)
1) il faut ordonner le polynôme suivant les puissances décroissantes de x (terme de degré 2, puis terme de degré 1 puis terme constant)
2) il est souhaitable soit
* de rédiger ("L'expression du bénéfice en fonction de x est ...."
* soit d'écrire une égalité du type : B(x) = ....
Quand je le tape sur ma calculatrice, je remarque que pour faire du bénéfice , il faut que l'entreprise doit vendre au maximum 76pièces
Est ce bien cela?
"Quand je le tape" c'est quoi que tu tapes ?
OUI pour 76 et cela confirme ce que tu peux voir GRAPHIQUEMENT
Et au minimum 23 pièces
Dans l'énoncé, on dit et on montre que x € [40;80]
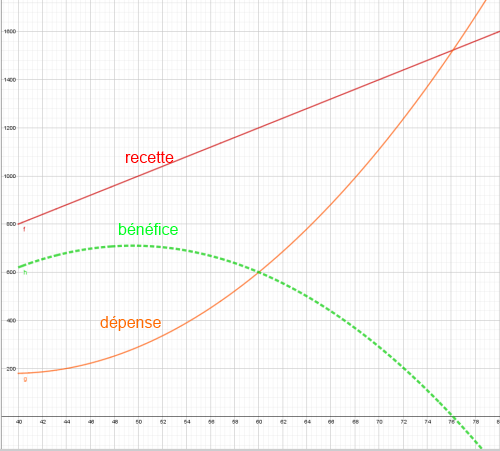
Je le tape dans l'option "table" de ma calculatrice
Oui vous inquiètez pas pour la rédaction je vais gerer 
Merci à tous pour votre aide
Je vous souhaite une très bonne année 2020 et une bonne santé