- Triangles : milieux et parallèles, théorème de Thalès
- Exercices sur les Triangles, milieux et parallèles
- Huit Exercices sur le théorème des milieux - quatrième
- 10 Exercices sur les équations et les mises en équations - quatrième
- Six Exercices sur les pourcentages - quatrième
- Cours sur les fractions suivis de six Exercices - quatrième
- Exercice de Calcul avec des fractions - 4ème
- Sept Exercices sur les fractions - quatrième
Inscription / Connexion Nouveau Sujet
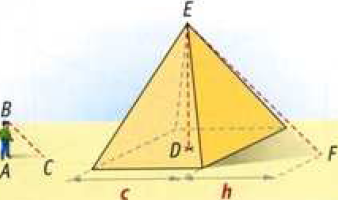
Thales attendit que son ombre soit exactement égale a sa taille .A cet istant ,il posa une pierre à l'extremité de l'ombre du sommet de la pyramide et meusura la longueur de l'ombre visible sur le sol.
Il trouva h=18 thales , l'unite de longueur etant le Thales avec AB qui est thales = 1 Thales .
La longueur d'un cotes du carré de base" de la pyramide est c=134 Thales
a)Calculer en Thalès, la hauteur de la
pyramide de Khéops
b) Sachant que thales = 1.73m calculer la hauteur de la pyramide en metre
*** message déplacé ***
Dm
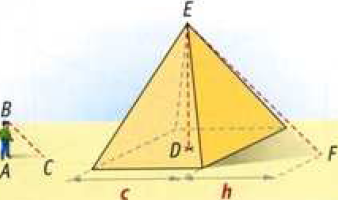
Thales attendit que son ombre soit exactement égale a sa taille .A cet istant ,il posa une pierre à l'extremité de l'ombre du sommet de la pyramide et meusura la longueur de l'ombre visible sur le sol.
Il trouva h=18 thales , l'unite de longueur etant le Thales avec AB qui est thales = 1 Thales .
La longueur d'un cotes du carré de base" de la pyramide est c=134 Thales
a)Calculer en Thalès, la hauteur de la
pyramide de Khéops
b) Sachant que thales = 1.73m calculer la hauteur de la pyramide en metre
Bonjour,
Ou est tu bloqué exactement ?
Voici quelques clés :
- Le soleil étant loin on peut considérer ses rayons comme parallèles. Donc (BC) // (EF). "Or (AC) et (DF) ont la même direction tout comme (BA) et (DE)"
Ainsi tu peux "décaler" (pour visualiser uniquement) le triangle ABC dans le triangle DEF pour pouvoir utiliser le théorème de Thales.
Du coup tu as (BA) // (DE) etc etc...
En gros il faut que tu travaille dans le triangle DEF et ABC.
Bonjour,
il faut utiliser les réductions
le triangle ABC est une réduction du triangle DEF dans le rapport k = AC/DF = AB/DE
reste à calculer DF pour connaitre ce rapport de réduction...
D est le centre de la base et les données "c" et "h" permettent de calculer DF immédiatement
"calculer en Thalès" veut dire "avec comme unité de longueur la taille de monsieur Thalès"
pas en utilisant un quelconque théorème de Thalès vu en 3ème seulement
merci vous m'avais déjà beaucoup aider mais je n'ai pas compris comment appliquer le théorème de Thalès dans cette pyramide et a quoi sert de savoir que (AB)//(DE). svp aider moi  :?
:? :?
:? :?
:?
on ne demande pas d'appliquer le théorème de Thalès du tout.
ceci (le théorème de Thalès) est une autre façon de résoudre le problème, qui ne peut être utilisée qu'en 3ème
en 4ème, niveau déclaré ici de cet exo, ce théorème n'est pas disponible.
et on peut parfaitement ne pas l'utiliser ni en parler du tout, comme j'ai dit
il faut comprendre que Thalès est un personnage et pas seulement un théorème
la mention de "Thalès" dans cer exo fait référence exclusivement à ce personnage, mathématicien Grec, et à sa taille qui est "par définition" de 1 Thalès
les longueurs sont toutes mesurées en Thalès dans l'énoncé et dans la question 1
si ça te choque de parler de "Thalès" comme étant une unité de mesure, remplace partout "Thalès" dans l'énoncé à chaque fois qu'il est fait mention d'une mesure par "schmurtz" :
... mesura la longueur de l'ombre visible sur le sol.
Il trouva h=18 schmurtz, l'unité de longueur étant le schmurtz, avec AB qui est 1 schmurtz .
La longueur d'un côté du "carré de base" de la pyramide est c=134 schmurtz
a)Calculer en schmurtz, la hauteur de la pyramide de Khéops
b) Sachant que 1 schmurtz = 1.73m calculer la hauteur de la pyramide en mètres


 :(
:(

