Bonjour, j'aurais besoin de votre aide pour un exercice de DM :

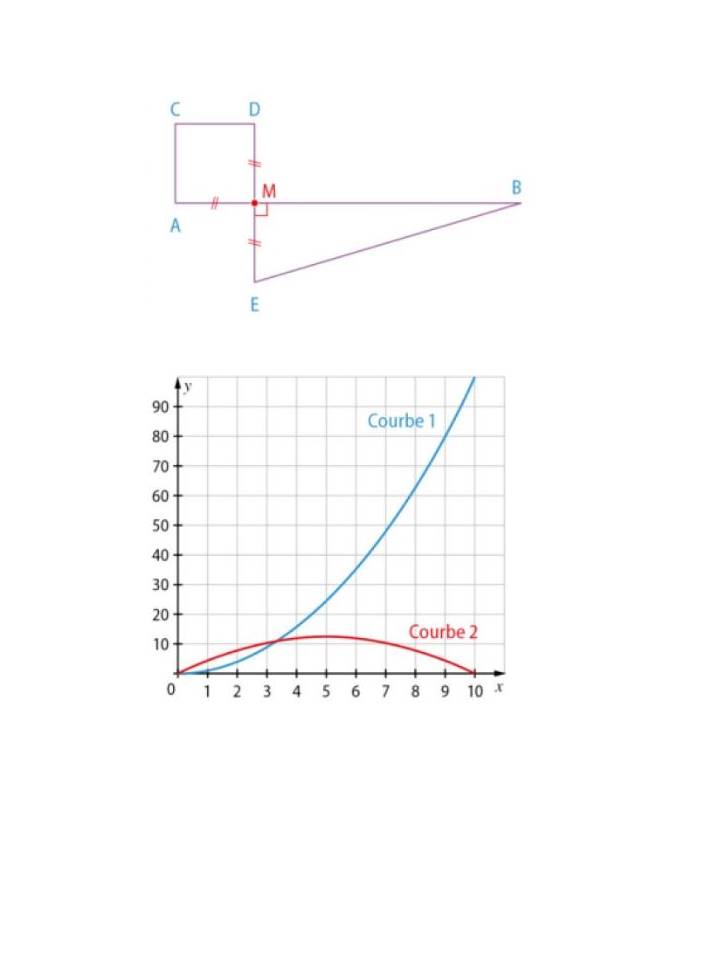
[AB] est un segment de longueur 10 cm et M est un point de ce segment distinct de A et B.
A chaque position du point M, correspond un carré AMDC et un triangle BME rectangle en M.
L'objectif est de savoir s'il existe une (ou plusieurs) position(s) du point M telle(s) que les aires du carré AMDC et du triangle BME soient égales.

1. Choisir trois positions différentes du point M et déterminer à chaque fois les valeurs de l'aire du carré AMDC et les valeurs correspondantes de l'aire du triangle BME. Ces valeurs permettent-elles de répondre à la question posée ?

2. On décide d'appeler x la longueur AM, f la fonction qui au réel x fait correspondre l'aire du carré AMDC et g la fonction qui au réel x fait correspondre l'aire du triangle BME.

a. A quel intervalle appartient x ?

b. Sur le graphique ci dessous, on a tracé les courbes représentatives des fonctions f et g.
   Quelle courbe représente la fonction f ? Justifier.

c. Utiliser ce graphique pour déterminer s'il existe un réel x tel que les aires de AMDC et BME soient égales. Donner un encadrement de ce réel par 2 entiers consécutifs.

Aidez-moi à résoudre cet exercice, je bloque !
Merci beaucoup de votre précieuse aide !