Inscription / Connexion Nouveau Sujet
Dm de maths représentation graphique d'une fonction et équation
Bonjour, j'ai un soucis avec mon dm de maths. Je ne comprends pas ce qu'il faut faire à cette question de mon dm :
2. Discutez selon les valeurs du réel "k" du nombre de solutions de l'équation f(x) = k.
On notera des phrases du type : Si k appartient à (intervalle ou union d'intervalle de R l'équation f(x) = k a ... solution(s).
J'ai bien-sûr un graphique qui correspond à cette fonction mais je ne peux pas vous l'envoyer. Donc je voudrais juste savoir est-ce que je dois chercher les antécédents ou les images possibles pour un nombre compris dans cet invervalle ? Je pars de quel axe (abscisse ou ordonnée) ? Voilà merci d'avance.
la FAQ du forumbonjour
à mon avis, sans énoncé complet (et la donnée de ce que représente f) cela doit dépendre de la vitesse du vent et de l'âge du capitaine ! 
Non en tout cas pas dans les données qu'on a. Mais du coup pour la question je ne sais pas si je dois chercher pour x ou pour k sur quel axe chercher et tout?
OK, donc pas de solution pour k=5
dit autrement il n'y a pas de x solution
pourquoi ?
parce que la droite d'équation y=5 ne coupe jamais la courbe de f
regarde ce dessin maintenant
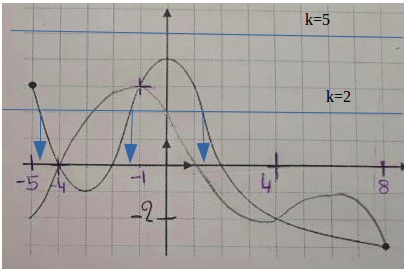
j'ai choisi k=2
la droite d'équation y=2 coupe 3 fois la courbe de f
et je lis sur l'axe des abscisses (fleches bleues) les 3 abscisses solution
donc à toi de regarder quels cas tu dois étudier pour avoir 0 solution au problème (c'est à dire 0 intersection), 1 solution, 2 solutions,, 3 solutions...
OK
voilà
Merci. Donc là j'ai fait ça est-ce que c'est bon :
Si k appartient à [-5 ; 8] alors l'équation f(x) = -3 n'a pas de solution
Si k appartient à [-5 ; 4] alors l'équation f(x) = -2 a 2 solutions
Si k appartient à [-5 ; 1 ] U [ 1 ; 8] alors l'équation f(x) = 3 a solutions
Si k appartient à [-1 ; 1] alors l'équation f(x) = 4 a 1 solution
Si k appartient à [-4 ; -2] alors l'équation f(x) = 1 n'a pas de solution
Voilà dites moi svp. Merci beaucoup
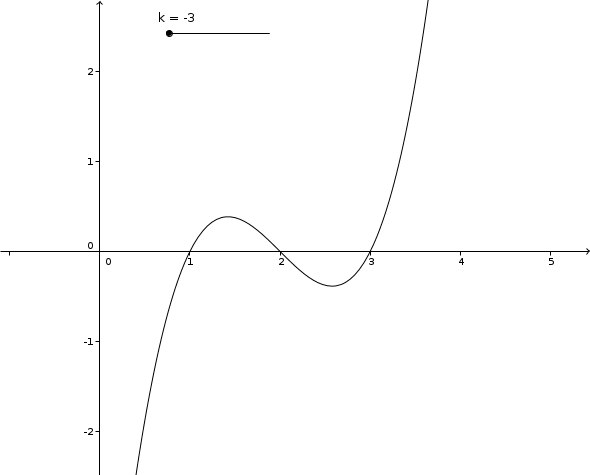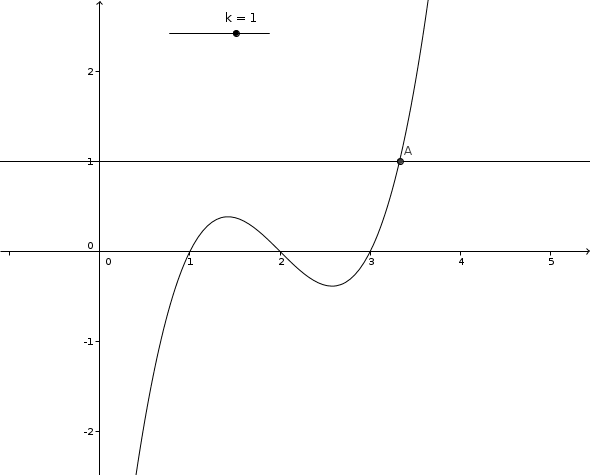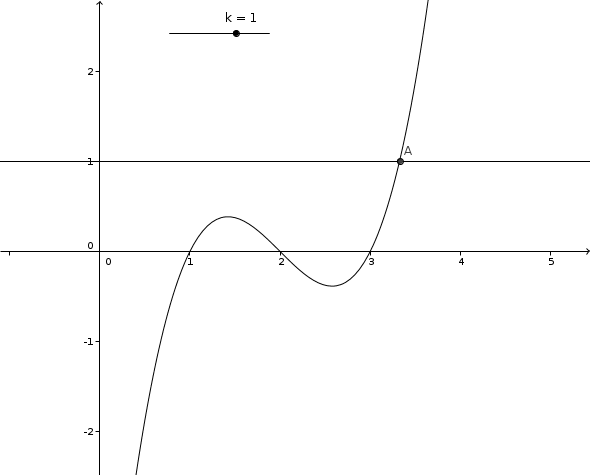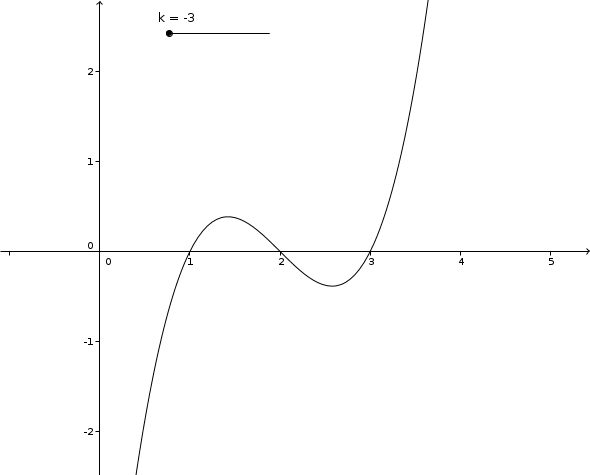
non, regarde je te montre avec une autre courbe
regarde ce qui se passe
tu vas voir suivant la valeur de k, qu'il y a 1 point d''intersection, puis 2, puis 3, etc...
la droite "horizontale qui bouge c'est y=k
toi tu peux mettre ta règle sur ton dessin pour faire la même chose
Merci mais je n'arrive pas à comprendre pourquoi les points A et B apparaissent ensemble et s'écartent. Bon j'essaye une dernière fois de proposer quelque chose :
Si k appartient à [4 ; 8] alors f(x) = k a 1 solution
Si k appartient à [-5; -1] alors f(x) = k a 2 solutions
Si k appartient à [-5 ; 4] alors f(x) = k a 4 solutions
Si k appartient à [-4 ; 2] alors f(x) = k a 4 solutions
Si k appartient à [-1 ; 2] alors f(x) = k a 3 solutions
Si il y a des fautes dans mes phrases est-ce que tu pourrais me les indiquer et me les corriger histoire de pouvoir les mettre dans ma copie parce que je commence vraiment à désespérer...
non, ce n'est pas bon, tu n'as pas compris le principe
tu confonds abscisse et ordonnée
que les points s'écartent ou se rapprochent, on s'en moque
c'est la droite rouge qui est intéressante et qui coupe ou pas ta courbe
et tu dois compter combien de fois ta courbe va être coupée par ta droite rouge
fais le sur ton dessin
toi, sur ton dessin
si k 
]-
; -3[ y-a-t-il des intersections ?
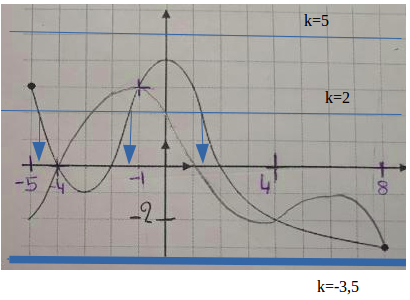
la "grosse" en bleue que je viens de remettre correspond à k=-3,5
crois tu vraiment que cette droite bleue coupe ta courbe ?
Mais là je ne comprends pas si ce qui nous intéresse c'est le x ou si c'est le cas, et si vous n'avez pas une méthode avec les mots images et antécédents pour mieux comprendre ? En fait est-ce que je dois quand même chercher un antécédent, une image ..?
Mais du coup quand je vais recopier sur ma copie f(x) = k je recopierai k comme ça je ne remplacerai pas k par un nombre ?
En fait ce qui me perturbe c'est que si on ne connaît pas la valeur de k alors on ne peut pas tracer de droite horizontale si on ne connaît pas sa valeur
k peut prendre toutes les valeurs possibles entre - et +
tant que ta règle ne sera pas arrivée à k=-3 (en arrivant de -), tu ne pourras jamais avoir d'intersection, puisque ton point le plus bas de ta courbe est positionné à une ordonnée de -3
et ensuite tu remontes doucement ta règle et tu comptes le nombre de points d'intersection
comprends-tu mieux ,
Oui mais du coup là sur le graphique j'ai délimité la zone en abscisse qui nous intéresse, mais alors je fais quoi vu que je ne connais pas où est k sur les ordonnées ? C'est ça que je ne comprends pas depuis le début
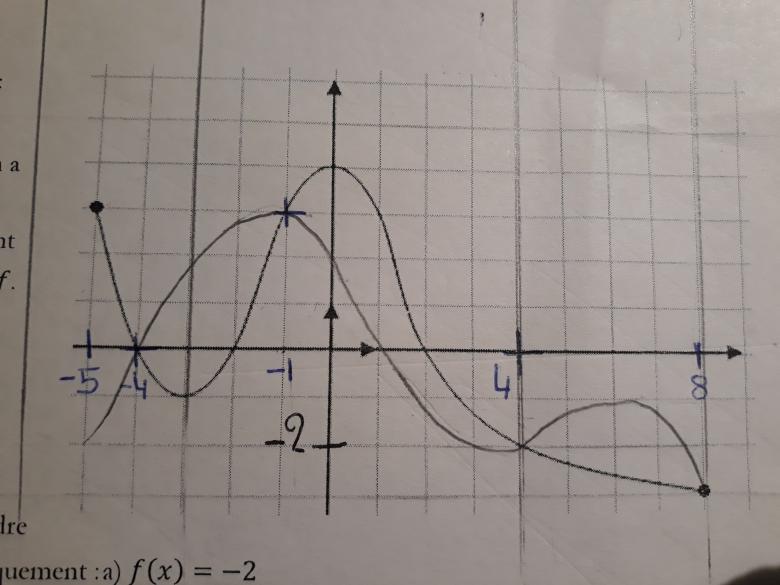
J'ai pris une photo coupée où on voit juste le graphique ça a bugé pour la dernière photo donc voilà là je fais quoi parce que je ne sais pas où k se situe sur les ordonnées. Je suis vraiment désespérée là je ne comprends pas est-ce que vous pourriez me faire un exemple que je pourrais mettre dans le dm ? Peut être que je comprendrai avec ça
si k ]- ; -3[ la droite d'équation y=k ne coupe pas la courbe donc f(x)=k admet 0 solution
si k=-3
la droite d'équation y=-3 coupe la courbe en un seul point (le point d'abscisse x=8)
donc l'équation f(x)=k admet une seule solution
etc
D'accord mais là vous êtes partie du fait que k = -3 pour le deuxième exemple en fait et c'est ça que je comprends pas parce que moi sur ma copie je suis censée mettre k tout simple et pas k = -3
Et pour le premier exemple je ne vois pas pourquoi k ne couperait pas la courbe parce que k peut être n'importe où sur l'axe des ordonnées
parce que k=-3 donne la 1re fois où la droite (la grosse bleue sur mon dessin) va rencontrer la courbe, donc il faut le dire !!
et ensuite k]-3 ; -2[ (-2 environ) toujours une seule intersection...
et lorsque k=-2 je vois 3 solutions
et tu continues comme ça....
Annuler
connectez vous