Inscription / Connexion Nouveau Sujet
Dm exercice 1
Bonjour, ceci est mon dernier exercice qui constitu mon Dm. Je voulais savoir si il est juste. Merci d'avance pour votre aide.
EXERCICE:
On considère une fonction f définit sur [ -2 ; 5] dont on donne ci-dessous le tableau de valeurs et le tableau de variations.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | 4 | 1 | -3 | 0 | 1 | 4 | 5,5 | 2 |
VOIR TABLEAU DE VARIATION CI-DESSOUS
1) Parmi les affirmations suivantes, lesquelles sont correctes ? Justifier quand elles
sont fausses.
a) Le maximum de f sur [-2 ; 5] est 5,5
b) f(1,5) < f(2,5)
c) L'équation f(x) = 4 admet exactement deux solutions : -2 et 3
d) L'équation f(x) = 1 admet exactement deux solutions : -1 et 2
e) Le minimum de f sur [-2 ; 5] est -3
2) Tracer une courbe représentant la fonction f sur [-2;5]
Voici mon travail :
a) Vrai
b) Vrai
c) Vrai
d) Vrai
e) Vrai
Je trouves cela très étrange, j'ai trouver que toute les affirmations était vrai, je pense que je suis tomber dans plusieurs pièges mais j'ignore ou.
En ce qui concerne la question 2, je ne sais pas comment poster ma courbe.
Ah oui, effectivement, je ne me suis concentrée que sur le tableau de valeurs.
a) Faux car le maximum de f sur [-2 ; 5] est 6
b) Vrai
c) Je ne vois pas mon erreur
d) Vrai
e) Vrai
Pour la d, f(x) =- 1 et 2 car cela est inscrit dans le tableau de variation
non, x n'as pas pour image 4 sur [3,5 ; 5]
Si vous prenez un entre 3, 5 et 5 la fonction décroît de 6 à 2 on passe donc forcément par 4
donc a bien une solution dans
c'est le même problème pour d mais comme on s'arrête à 2 et qu'1 est plus petit il n'y en a donc pas
On ne vous demande pas la valeur
on vous affirme qu'entre et 5 l'équation
n'a que deux solutions
c'est faux puisqu'il y en a une troisième entre 3,5 et 5. Peu me chaut la valeur je prouve qu'elle existe.
Ah d'accord il y a donc 2 intervalles.
En ce qui concerne la courbe, comment puis je vous l'envoyer ?
Je peux vous l'envoyer cette après midi ?
Non c'est bon je pense avoir comprit mais comment le rédiger?
c) Faux car f(x) = 4 également sur l'interval [3,5 ; 5]
Par exemple. Faites attention on a l'impression d'avoir un petit segment à 3, parallèle à l'axe des ordonnées C'est impossible par définition d'une fonction
Un autre exemple mais il a aussi un défaut au voisinage du maximum Il faudrait le relier plus rapidement au point suivant
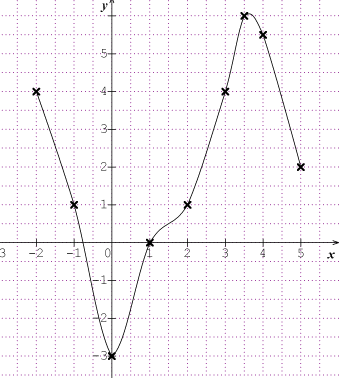
D'accord, je vais la refaire mais plus espacés et plus lissible. Merciiiii infiniment pour votre aide. Il me semble que c'était vous qui m'aviez lors de mon dernier. Si, oui et bien sachez que j'ai eu 19/20 donc merciiii beaucoup