Inscription / Connexion Nouveau Sujet
DM FONCTION 2nd
Vois-ci l'exercice concerné, il me parait impossible à faire, j'ai beau cherché dans mes cours, faire des brouillons, je n'y parvient pas..
C'est pour ce-là que je m'adresse à vous en espérant trouver de l'aide..
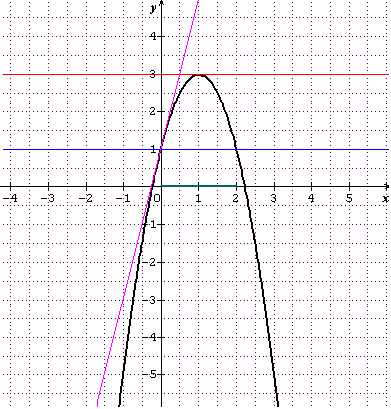
Soit F la fonction définie sur R par f(X) = -2x²+4x + 1, dont la courbe représentative C dans un repère orthonormé est donnée ci-contre.(Faire une hypothèse)
1) Conjecturer les variations de f.
2) Démontrer que pour tout X de IR, F(X) = 3-2(x-1)².
3) Étudier les variation de F sur ]-infini;1]
4) Représenter sur le graphique les solutions de f(x) = 3 et f(x)>1 puis résoudre algébriquement ces équations.
5) Soit x un réel compris entre -2 et 0
a) Encadrer f(x) en utilisant les variations de f.
b)Encadrer -2x2 puis 4x+1. En déduire un encadrement de f(x).
6) Tracer la droite d'équation y=4x+1.
Représenter sur le graphique les solutions de F(x) =4x+1 puis résoudre algébriquement cette équation.
Bonjour,
1) Tu affiches la fct sur ta calculatrice et tu conjectures que :
f(x) est croissante sur ]-inf;1[ et décroissante sur ]1;+inf[
2) Démontrer que pour tout X de IR, F(X) = 3-2(x-1)²
Tu développes :
3-2(x-1)²
et tu vas retrouver :
-2x²+4x + 1
Je vais t'envoyer la suite...si personne ne l'a fait déjà.
3)
Soient a < b 
1
a-1 < b-1 1-1
a-1 < b-1 0--->ligne (1)
On est donc dans les nbs négatifs. Or :
Sur ]-
;0] , la fct carrée est décroissante , ce qui veut dire que pour :
x1 < x2 , on a : f(x1) > f(2)
Donc en élevant les termes de (1) au carré , il faut changer le sens de l'inégalité.
(a-1)² > (b-1)² 
0-->ligne (2)
On va multiplier les termes de (2) par "-2" qui est négatif , donc il faut changer à nouveau le sens de l'inégalité.
-2(a-1)² < -2(b-1)² 0
On va ajouter 3 qui ne change pas le sens de l'inégalité.
3-2(a-1)² < 3-2(b-1)² 3
Soit :
f(a) < f(b) 3
On est parti de a < b pour arriver à f(a) < f(b). Or :
f est strictement croissante si pour a < b dans un intervalle donné on a f(a) < f(b) .
Donc sur ]-;1] , f(x) est strictement croissante .
4) Représenter sur le graphique les solutions de f(x) = 3 et f(x)>1 puis résoudre algébriquement ces équations
Tu verras sur le graph plus bas la droite y=3 en rouge.
On résout :
3-2(x-1)²=3
Tu dois trouver : x=1
f(x)>1
Sur le graph, ce sont les abscisses des points de Cf au-dessus de la droite bleue y=1.
Solution en vert sur axe des x.
On résout :
-2x²+4x + 1 > 1
soit :
-2x²+4x > 0
x(-2x+4) > 0
Il faut que tu fasses un tableau de signes . Tu vas trouver :
S=]0;2[
5) Soit x un réel compris entre -2 et 0
a) Encadrer f(x) en utilisant les variations de f.
On a vu que : sur ]-
;1] , f(x) est strictement croissante .
Donc sur [-2;0] , f(x) est strictement croissante , ce qui donne pour x compris entre -2 et 0 :
f(-2)
f(x) f(0)
Calcule f(-2) et f(0).
b)Encadrer -2x² puis 4x+1. En déduire un encadrement de f(x).
Sur [-2;0], la parabole y=x² nous montre que :
0
x² 4
On multiplie par -2 qui est négatif donc :
0
-2x² -8
que l'on va plutôt écrire :
-8
-2x² 0--->ligne (3)
Sur [-2;0] :
-2
x 0
On multiplie par 4 qui est positif donc :
-8
4x 0
On va ajouter 1 qui ne change pas le sens de l'inégalité.
-7
4x+1 1--->ligne (4)
On ajoute membre à membre (3) et (4) :
-8-7
-2x²+4x+1 0+1
Donc sur [-2;0] :
-15
f(x) 16) Tracer la droite d'équation y=4x+1.
Elle est en rose.
Représenter sur le graphique les solutions de F(x) =4x+1
Tu lis l'abscisse de l'intersection de la droite y=4x+1 et de Cf.
puis résoudre algébriquement cette équation.
On résout :
-2x²+4x + 1=4x+1
Tu le fais.
Annuler
connectez vous