Ok, attends que je rédige le corrigé. Tu dois le rendre pour quand ton DM?

Bonjour,

question 1 : niveau 4ème
question 2 : il n'est pas difficile de voir le facteur commun x-3
de toute façon "monter que résultat donné" peut aussi se faire autrement :
en développant aussi (x-3)(4x-5) et en vérifiant si ça donne la même chose.
(pfff on vous entraine à ne PLUS penser en vous donnant ainsi les réponses dans les énoncés)

calculer f(0) c'est remplacer x par 0 dans une des expressions de f(x).
laquelle donnera les calculs les plus simples ?
est-ce l'expression initiale ? la forme développée ? la forme factorisée ?
c'est ça qu'on te demande "en utilisant la forme de f(x) qui convient le mieux"
pareil pour les autres valeurs ou questions

4) la courbe se trace en plaçant quelques (en nombre suffisant) points de la courbe et en les reliant "à main levée" par une courbe "harmonieuse" (sans angles)

les traits de construction sont les traits "matérialisant" les points choisis, et matérialisant ce que veut dire une équation comme f(x) = 15 etc ...

Je dois le rendre le 29 et merci beaucoup

la réponse de MichelBL était ironique (smiley) si tu ne l'avais pas comprise,

on ne te donnera pas le corrigé
ici c'est un forum d'aide
et donc c'est à toi de faire quelque chose, de dire précisément ce qui te pose problème (et la réponse "tout" n'est pas acceptable vu le "niveau" des questions 1 et 2)
l'aide consiste à corriger et t'expliquer tes erreurs et te donner des indications pour te débloquer
un "corrigé" n'est en aucun cas une aide.
même si certains le comprennent ainsi et supposent la bonne foi du demandeur en présence d'un tel corrigé = supposent que le demandeur refait réellement l'exo "de lui même", ce qui est purement utopique.

la seule réponse attendue aux messages précédents était en fait un truc du genre
j'ai fait la question1 et j'ai trouvé ...
je ne vois pas le facteur x-3 dans x² - 9
j'ai fait les premières questions mais je ne sais pas quelle forme choisir pour résoudre f(x)=15
etc etc
bref des messages constructifs sur le travail que tu dois faire.

1) f(x)=x-3+2(x-3)²+x²-9
       = x-3+3(x²-6x+9)+x²-9
       =x-3+3x²-18x+27+x²-9
       =4x²-17x+15  

2)Il suffit de montrer que si on développe f(x)=(x-3)(4x-5), on retombe sur 4x²-17x+15.
(x-3)(4x-5)=4x²-5x-12x+15=4x²-17x+15;

3)

a. f(0)=4*0-17*0+15=15
et f(5/4)=4(5/4)-17(5/4)+15=(20/4)-(85/4)+15=20-(85/4)=(-5/4)=-1.25

b. On doit calculer f(x)=0 soit (x-3)(4x-5)=0
soit pour (x-3)=0,x=3 et pour (4x-5)=0 , x=(5/4)
Graphiquement cela signifie que la parabole coupe l'axe des abscisses pour x=3 et x=(5/4).Tu peux vérifier sur ta calculatrice graphique ou sur le logiciel Geogebra si tu veux.

c) Calculer f(x)=15 graphiquement cela reviendrait tout simplement à tracer une fonction constante y=15 et à observer pour quel valeur de x la fonction f(x)=15 coupe la fonction 4x²-17x+15.
Algébriquement cela revient à calculer pour quel valeur de x f(x)=g(x)
On doit donc calculer f(x)-g(x)=0.
La forme la plus simple à utiliser pour calculer ceci est (x-3)(4x-5)-(-15)=0, mais sache qu'on pourrai très bien partir de 4x²-17x-15-(-15)=0 et dans ce cas on obtiendrai 4x²-17x=0,qui serai moins facile à résoudre que (x-3)(4x-5)-(-15)=0;(en effet il faudrait la transformer sous la forme canonique puis utiliser différentes propriétés des identités remarquables etc... en fait tu retomberai sur (x-3)(4x-5)-(-15)=0)
Bon j'espère ne t'avoir pas trop embrouillé! calculons (x-3)(4x-5)-(-15)=0
On obtient x=0 et x=4.25
Cela signifie qu'aux points d'abscisses x=0 et x=4.25, la fonction constante y=15 coupe la fonction (x-3)(4x-5).
d. f(x)>0 cela revient donner l'intervalle pour lequel la fonction est strictement au-dessus de 0.
Or auparavant on a calculé f(x)=0.
On a f(x)>0 pour l'intervalle ]-;1.25[]3;+[

4)Cela est très simple;je te laisse le faire sur papier. J'ai essayé de t'envoyer ce que ça donnerai sur geogebra, mais le fichier était trop volumineux
N'hésite pas à reformuler le corrigé.
A plus

Merci beaucoup je t'en suis très reconnaissante, bonne après midi et merci encore!

reconnaissante d'avoir entièrement fait l'exo à ta place
tu crois que ça va t'aider à comprendre réellement ce que tu fais, de lire ainsi passivement au lieu de faire ??

m'enfin comme il y a des erreurs, ça n'est "pas si grave" ... trouver ces erreurs fera office de faire l'exo.
(et je ne parle pas des lourdeurs de rédaction et des réponses "à côté de la plaque" ou pas justifiées)


MichelBL :

Si sa manière de m'aider ne te conviens pas, évite de poster des commentaires et vas "aider" d'autres personnes qui ont sûrement besoin de toi. Sur ce bonne après midi et merci pour tes critiques très instructives.

à Mathafou:

Je suis tout à fait d'accord avec toi par rapport aux commentaires macho de mathafou ahah et merci pour tous ces précieux conseils qui vont m'être très utiles.
Je pense aller en ES mais je ne suis pas tout à fait décidée, mes parents auraient préféré que j'aille en S, mais je ne suis pas très alaise en maths.. :/

je te conseilles d'aller voir ce site génial ou un prof de math t'explique tout de A à Z:    http://cours2nde.blogspot.fr/
Disons que le fait de choisir la filière S te donnes beaucoup de débouchés après le bac, ce qui n'est pas le cas de ES et encore moins L.
Autrement voici ma chaîne youtube: https://www.youtube.com/user/michel8887, je pourrai éventuellement rédiger des   vidéoes de maths pour les 2nde quand j'aurai un petit peu de temps.

D'accord d'accord merci beaucoup! Et oui faire des vidéos pour les secondes serait vraiment top! Je peux toujours en parler a quelques amis à moi? Encore merci pour les sites et tes conseils ect..

savoir programmer c'est très bien, mais ne pas savoir utiliser les outils de base d'un ordinateur (traitement d'images ici) ne plaide pas en ta faveur.
on peut et c'est très largement suffisant, mettre tout ce qu'on veut comme images ici.
et mettre un fichier de 12 megapixels (3000x4000) destiné à être affiché au sein d'une page Web de forum est réellement aberrant !!
et si tu n'en tiens pas compte dans tes programmations de pages Web et bien c'est vraiment très dommage pour leur qualité.


ceci dit tu n'as tout de même pas trouvé ta propre erreur dans ce que tu as écrit
relis toi, il y a dans ta correction une absurdité manifeste, que ElisaGinot risque fort de ne pas trouver, devant une telle "correction toute rédigée" (pourquoi chercher à réfléchir si c'est tout cuit)

maintenant ici on a le droit d'exprimer son opinion. et parfaitement, je trouve que donner des corrections toutes faites n'est PAS aider et je le dis chaque fois que je peux. Mais je ne vois pas le rapport avec le niveau d'étude ni "être macho".

tu as parfaitement le droit de ne pas être d"accord là dessus
sachant que cette opinion est "équitablement" partagée en environ deux sortes d'intervenants sur l'ile :
ceux qui aident en expliquant pourquoi et en forçant le demandeur à faire lui-même l'exo
et ceux qui pour diverses raisons considèrent que ça ne sert à rien de se casser la nenette ainsi, et que de toute façon autant donner la correction tout de suite.

ce n'est de façon très officielle pas le but de ce forum (lire les règles)

N'hésites surtout pas à venir me poser des questions en maths sur ma chaîne dans la rubrique discussion afin que je puisse avoir des idées pour des vidéos de maths niveau 2nde. par exemple "Comment démontrer colinéarité de vecteur?" ou "Relation de chasle" etc ... à plus

daccord je n'hésiterai pas c'est entendu merci encore a plus

à mathafou: j'imagine que t'a dût prendre ta retraite pour avoir ainsi le temps de poster des messages inutiles et n'ayant riens à voir à l'exercice Franchement bravo En même temps t'a 66 ans c'est pas tous jeune ça Enfin bon je vais arrêter de perdre du temps à répondre à un vieux crouton comme toi. Pour l'absurdité tu n'arrêtes pas de m'en parler sans même me dire ou elle est ... honnêtement ce serait plutôt sympa de me la dire.Car ça arrive à tout le monde de faire des erreurs.

à dire que 0 = -1.25 dans
d'une part le calcul de f(5/4)
d'autre part la résolution deux lignes plus loin de f(x) = 0

et cela montre bien que ta réponse à la question 3a n'est pas celle qui est attendue

utiliser la forme la mieux adaptée pour calculer f(5/4)
la forme la mieux adaptée n'est certainement pas la forme f(x) = 4x²-17x+15 (surtout quand on oublie d'élever x au carré)

comme cela apparait à la question 3b, la forme la plus adaptée pour calculer f(5/4) est la forme factorisée.

pour la 3c c'est bien réellement la forme développée qui est la mieux adaptée et rien d'autre (il est inutile d'invoquer des formes canonique et de se lancer dans des calculs fumeux)
pour résoudre f(x) = ax² + bx + c = c la "forme adaptée" semble évidente : après simplification, on va pouvoir factoriser "instantanément" par x et obtenir une "équation produit nul"

3d) réponse incomplète (sans justifications)
tu affirmes gratuitement un truc de 1ère (alors qu'on est ici au niveau seconde) sur le cours du signe du trinome
ici on doit en fait effectivement utiliser la forme factorisée f(x)= (x-3)(4x-5) pour étudier le sign
et cette étude de signe ne se fait pas en affirmant un théorème de 1ère, mais en effectuant réellement un tableau de signes du produit.
et donc en concluant avec le même résultat bien entendu, mais cette fois justifié, au niveau seconde)

enfin la courbe via Geogebra se met ici sans aucun problème :

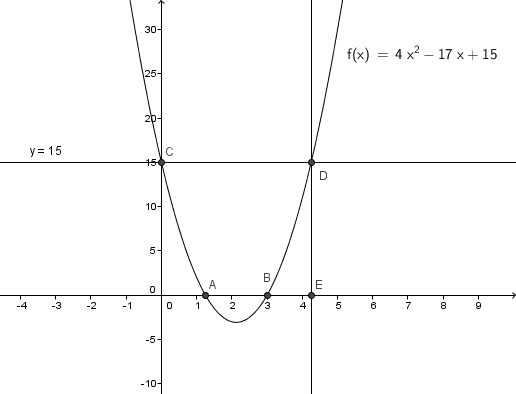
Qu'il est joli le graphique réalisé avec Geogebra.
Pour la 3a c'est vrai que je me suis trompé.j'ai rédigé rapidement la correction, et j'ai fait des fautes de frappes et de logique.
Pour la 3c, je voulais tout simplement lui dire qu'on pouvais retrouver la forme factorisée à partir de 4x²-17x+15

Quoi qu'il en soit, on a pas besoin d'un tableau de signe pour résoudre f(x)>0, on sait que "a" est positif, donc immédiatement on voit une courbe tournée vers le haut. On en déduit que tout f(x) compris entre ]1.25;3[ , n'est pas du signe de a etc ... De plus on peut assez facilement conjecturer avec une calculatrice graphique afin de vérifier ses résultats.

dsl ElisaGinot pour l'erreur à la question 3a

le "on sait" est en première à mon avis, pas en seconde.
tout au moins pas vraiment dans un exo "découverte" où on demande "la forme la plus adaptée pour.."