Inscription / Connexion Nouveau Sujet
DM geométrie en fonction de x
Bonjour à toute et à tous
j'ai un dm de math a rendre pour le mardi 5 mais j'ai du mal avec cette exercices, pouvez vous m'aidez s'il vous plait, merci d'avance
exercice:
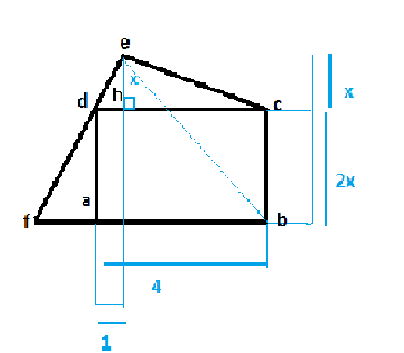
ABCD est un rectangle de longueur 4 et de largeur 2x
EDH est un triangle de hauteur EH tel que EH = x et DH = 1
la droite (DF) coupe la droite (AB) en F
1)
a) calculer, en fonction de x, l'aire du rectangle ABCD
b) calculer l'aire du triangle BCE
c) calculer en fonction de x, l'aire du polygone ABCED
2)
a)calculer DE et EC en fonction de x
b) en déduire, en fonction de xn le périmètre du polygone ABCED
3) démontrer que AF = 2
voici ce que j'ai fait: (dsl c'est très peut...)
1)
a) aire rectangle = L
l (Longueur largeur)
aire ABCD = 42x
= 8x
l'aire ABCD est de 8x
b) aire triangle = bh (base hauteur)
aire BCE = ....
CB = 2x CE = ? EB = ? ----> je crois que SOCATOA est envisageable ici, non ?
c) aire polygone: ....
ici le polygone est constitué d'un rectangle (ABCD) et d'un triangle (DEC)
donc aire polygone = aire rectangle + aire triangle
aire ABCED = 8x + ...
2)
a)je ne voit pas comment on peut calculer une droite --'
b) le périmètre du polygone ABCED = AB + BC + CE + ED + DA
(DA = 2x + x donc = 3x)(HC = 4 - 1 donc 3)
périmètre ABCED = 4 + 2x + EC + DE + 3x
= 4 + 5x + EC + DE
= ......
3) comment je suis censée mis prendre ??
Bonsoir,
Attention, Aire (triangle)=(base*hauteur)/2
Pour le triangle BCE, on connait la base BC=2x
Il est facile de connaitre la hauteur issue de E (elle est parallèle et égale à HC)
Bonsoir,
Ton énoncé n'est pas tout à fait en concordance avec la figure que tu as faite.
Je me base donc sur la figure
aire ABCD exact
aire BCE si tu mènes par E la perpendiculaire à [BC], tu vois que sa longueur est égale à HC dont la longueur est de 3
l'aire du triangle BCE sera donc de 3*2x/2=3x
aire ABCED aire du carré ABCD + aire DEC= 8x+4x/2=10x
DE par Pythagore dans DEH= 
(x²+1)
EC par Pythagore dans HEC=(9+x²)
le périmètre de BCEDA en découle
EF: les triangles EHD et DAF sont semblables.
Et comme le rapport AD/EH=2x/x=2
le rapport AF/DH sera également de 2
et comme DH=1
AF=2
Bonsoir
énoncé : c'est la droite (ED) coupe la droite (AB) en F et non la droite (DF) coupe la droite (AB) en F
*
1)b)
aire du triangle BCE = base*hauteur/2 = BE*3/2 =3x
c)
aire du polygone ABCED = aireABCD+aireDEC =8x + 4*x/2= 10x
2)
a) DE = (x²+1) (Pythagore)
EC = (9+x²)
b) le périmètre du polygone ABCED = 4 + 2x +(9+x²) + (x²+1) + 2x = ...
3)
appliquer Thalès dans les triangles DAF et DHE
A+
bonsoir a tous
d'abord, merci beaucoup à vous de votre aide
Aire (triangle)=(base*hauteur)/2
DE par Pythagore dans DEH=
(x²+1)
EC par Pythagore dans HEC=
(9+x²)
le périmètre de BCEDA en découle
(9+x²) + (x²+1) ??ah non excusez moi je n'avais pas vue votre commentaire geo3
je doit donc faire 4 + 2x +(9+x²) + (x²+1) + 2x = ... ??
Annuler
connectez vous