Annuler
connectez vous
- Arithmétique : divisibilité, PGCD et PPCM, Nombres premiers
- Des mathématiciens célèbres : Fermat et Gauss
- Fonction exponentielle - Fiche de Cours terminale
- Le raisonnement par récurrence : principe et exemples rédigés
- Limites de fonctions - Cours sur les limites
- Fiche sur les nombres complexes - terminale
- Cours sur les suites en Terminale S
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale ArithmétiqueTopics traitant de Arithmétique [tout]Lister tous les topics de mathématiques
Niveau terminale
Dm Math - Matrix
Posté par Kaimoon
Salut,
J'ai une sujet de math au desous.
On lance 100 fois une pièce bien equilibree. On se demande quelle est la probabilite p d'obtenir au moin six lancers consecutifs identiques.
1. À votre avis, a-t-on plutôt:
p <1/3; 1/3=<p<2/3; p>=2/3
Je pense que p >= 2/3
2a) Simuler le lancer de 100 pieces sur une calculatrice ou un logicel. Obtenz-vous au moins 6 lancers consecutifs identiques?
- Quelle loi je peux appliquer? J'essaie la loi binomiale avec n = 100, p = 0.5, k <=6.
b) recommencezune dizaine de fois. Maintenez-vous votre conjecture?
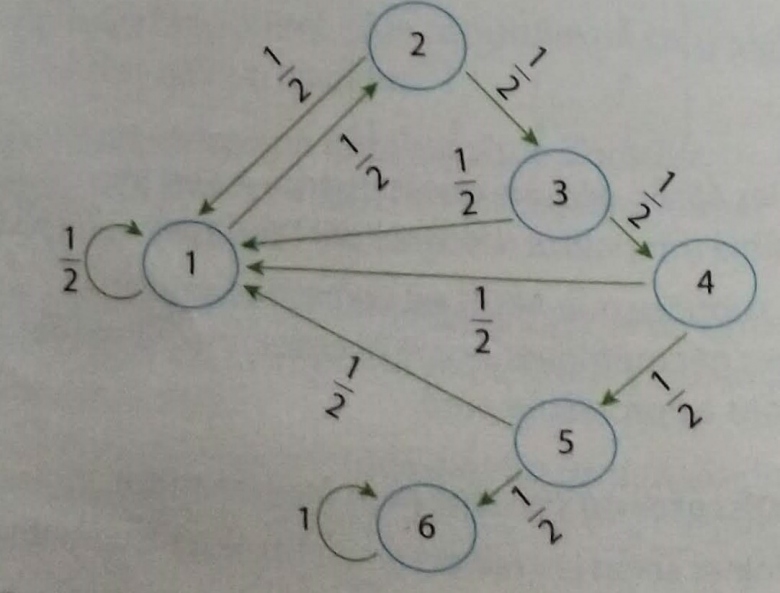
3. On illustre l'évolution de la situation par un graphe à six sommets ou le "sommet k" correspond a k lancers consecutifs identiques.
a)Expliquer les probabilités portées sur ce graph.
b)Ecrire la matrice de transition T associée à ce graphe dans l'ordre croissance des valeurs de k.
4. On designe par Xnla matrice donnant l'état probabiliste après n lancers pour n>=1.
a) Justifier que X1 = (1 0 0 0 0 0).
b) Déterminer à la calculatrice ou avec un logiciel la matrice donnant l'etat probabiliste apres lé 100 lancers
c) En déduire une réponse à la question posée
5.Adapter la méthode précédente pour connaître la probabilité d'avoir
a) Au moins 6 tirages consecutifs identiques sur 200 lancers
b) Au moins 8 tirages consecutifs identiques sur 100 lancers
salut
et alors ? tu en es où ?
PS : et tu penses mal ...
déjà avec six lancers obtenir six fois la même face a pour probabilité 1/2^6 << 1/3
(il y a bien sur indépendance)
salut
rapidement on peut ecrire à partir du graphe en utilisant les probabilités totales que
P(1n+1)=P(1n+1/1n.P(1n)+ P(1n+1/2n.P(2n)+P(1n+1/3n.P(3n) +.....
P(1n+1/6n.P(6n) et faire pareil pour P(2n+1),
P(3n+1) ....et pour P(6n+1)
flight @ 14-02-2019 à 18:54
salut
rapidement on peut ecrire à partir du graphe en utilisant les probabilités totales que
P(1n+1)=P(1n+1/1n.P(1n)+ P(1n+1/2n.P(2n)+P(1n+1/3n.P(3n) +.....
P(1n+1/6n.P(6n) et faire pareil pour P(2n+1),
P(3n+1) ....et pour P(6n+1)
salut
rapidement on peut ecrire à partir du graphe en utilisant les probabilités totales que
P(1n+1)=P(1n+1/1n.P(1n)+ P(1n+1/2n.P(2n)+P(1n+1/3n.P(3n) +.....
P(1n+1/6n.P(6n) et faire pareil pour P(2n+1),
P(3n+1) ....et pour P(6n+1)
Hello,
C'est la repondre pour la question 3a)?
carpediem @ 14-02-2019 à 17:18
salut
et alors ? tu en es où ?
PS : et tu penses mal ...
déjà avec six lancers obtenir six fois la même face a pour probabilité 1/2^6 << 1/3
(il y a bien sur indépendance)
.
salut
et alors ? tu en es où ?
PS : et tu penses mal ...
déjà avec six lancers obtenir six fois la même face a pour probabilité 1/2^6 << 1/3
(il y a bien sur indépendance)
Merci de votre réponse.
Je suis en train de faire la 3eme question
carpediem @ 15-02-2019 à 10:02
alors la suite est élémentaire ...
alors la suite est élémentaire ...
Pardon, Que voulez-vous dire.
Mai comment peut-on-faire la matrice de transition T associée à ce graphe dans l'ordre croissance des valeurs de k
donc tu n'as pas compris ce graphe ...
je te donne les deux premières colonnes
si k = 1 alors soit le nombre de même face passe à deux (k = 2) soit on change de face et retombe à k = 1
1/2 1/2
1/2 0
0 1/2
0 0
0 0
0 0
C'est ca?
1/2 1/2 1/2 1/2 1/2 1/2
1/2 0 1/2 1/2 1/2 1/2
0 1/2 0 1/2 1/2 1/2
0 0 1/2 0 1/2 1/2
0 0 0 1/2 0 1/2
0 0 0 0 1/2 1/2
1/2 1/2 1/2 1/2 1/2 1/2
1/2 0 1/2 1/2 1/2 1/2
0 1/2 0 1/2 1/2 1/2
0 0 1/2 1/2 1/2 1/2
0 0 0 1/2 0 1/2
0 0 0 0 1/2 1/2
faux ...
la somme des termes de chaque colonne fait 1 (c'est des probabilités)
quand tu as eu 5 fois la même face tu ne reviens pas à 2 fois la même face ou l'autre ...
ok
1/2 1/2 1/2 1/2 1/2 1/2
1/2 0 0 0 0 0
0 1/2 0 0 0 0
0 0 1/2 0 0 0
0 0 0 1/2 0 0
0 0 0 0 1/2 0
0 0 0 0 0 1/2
carpediem @ 15-02-2019 à 12:31
non !! tu as 7 lignes !!
non !! tu as 7 lignes !!
C'est ma faute.
1/2 1/2 1/2 1/2 1/2
1/2 0 0 0 0
0 1/2 0 0 0
0 0 1/2 0 0
0 0 0 1/2 0
0 0 0 0 1/2
ben X_1 : évident !!
tu lances la pièce une fois donc tu as obtenu soit un pile soit une face ...
ben tu calcules T^100 * X_1 ou simplement T^100 ...
carpediem @ 17-02-2019 à 10:16
ben X_1 : évident !!
tu lances la pièce une fois donc tu as obtenu soit un pile soit une face ...
ben tu calcules T^100 * X_1 ou simplement T^100 ...
ben X_1 : évident !!
tu lances la pièce une fois donc tu as obtenu soit un pile soit une face ...
ben tu calcules T^100 * X_1 ou simplement T^100 ...
Mais comment On prove X1 = 1 0 0 0 0 0 ?