Inscription / Connexion Nouveau Sujet
DM maths
bonjour j'aurais besoin d'aide svp merci d'avance
histoire des mathématiques
Carl Friedrich Gauss, à l'âge de 9 ans a été puni par son maître d'école . Cdernier pensant l'occuper un long moment lui a demandé d'additionner tous les nombres entiers compris entre 1 et 100.Mais quelques minutes plus tard le petit Carl revient et lui donne la bonne réponse!!
voici la méthode:
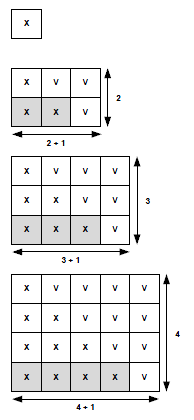
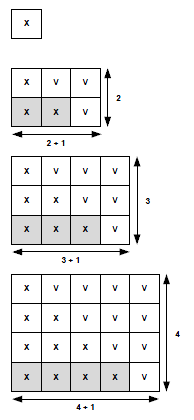
il a représenté les entiers par des croix qu'il a placées sous une forme triangulaire:
en ligne 1,1 croix pour le nombre 1 x
en ligne 2,2 croix pour le nombre 2 x x
etc.
il s'est aperçu que pour calculer 1+2 il suffisait de compléter son triangle en un rectangle ayant une croix de plus en longueur .1+2 était alors le résultat de l'aire de rectangle divisé par 2 x v v
x x v
pour calculer 1+2+3 il a fait le même raisonnement qui fonctionne encore ! x v v v
x x v v
x x x v
1.vérifier le raisonnement de Gauss pour 1+2 puis 1+2+3.
2.pour 1+2+...+100 quelles sont les dimensions du rectangles qui permet de trouver la bonne réponse? en déduire la réponse de Gauss au maître d'école.
3.on additionne tous les entiers consécutifs de 1 jusqu'à un entier quelconque noté n.
que vaut cette somme (en fonction de n)
Bonjour
Question 1 :
A partir du dessin :
Pour N=2, on a un rectangle de surface S = (2 + 1) x 2 = 3 x 2 = 6 carrés
donc S / 2 = 3 et on remarque que 1 + 2 = 3
Pour N=3, on a un rectangle de surface (3 + 1) x 3 = 4 x 3 = 12 carrés
donc S / 2 = 6 et on remarque que 1 + 2 + 3 = 6
Pour N=4, on a un rectangle de surface (4 + 1) x 4 = 5 x 4 = 20 carrés
donc S / 2 = 10 et on remarque que 1 + 2 + 3 + 4 = 10
Etc.
Question 2 : S = 1 + 2 + 3 + 4 + ... + 100 ?
Pour N=100, on a un rectangle de surface (100 + 1) x 100 = 101 x 100 = 10100 carrés
donc S / 2 = 5050 donc la somme 1 + 2 + 3 + 4 + ... + 100 = 5050.
Question 3 : S = 1 + 2 + 3 + 4 + ... + n ?
S = n (n + 1)
rebonjour et excuse-moi pour ce long silence.
Ma dernière formule comme l'a écrit ListenAicha.
J'ai oublié de diviser par 2.
La réponse est donc :
On va reprendre avec des petits exemples (je ne suis pas assez doué pour te produire de beaux dessins  ). Je me permets donc de prendre ceux de bbomaths
). Je me permets donc de prendre ceux de bbomaths
Maintenant, allons jusqu'à 5 :
xvvvvv
xxvvvv
xxxvvv
xxxxvv
xxxxxv
La longueur est de 5, la largeur de 5+1, l'aire est donc égale à 5*6=30
Tu remarques que la longueur correspond au dernier terme de la somme, la largeur c'est la longueur +1
Nous faisons donc la somme jusqu'au nombre .
Avec le même raisonnement que précédemment, la longueur est donc égale à , la largeur est donc égale à
, l'aire est égale au produit puisque c'est un rectangle
Il ne reste plus qu'à diviser ce produit par 2
je te remercie ton explication m'a aidé cette fois a bien comprendre encore merci et désolé d' avoir du encore te déranger



