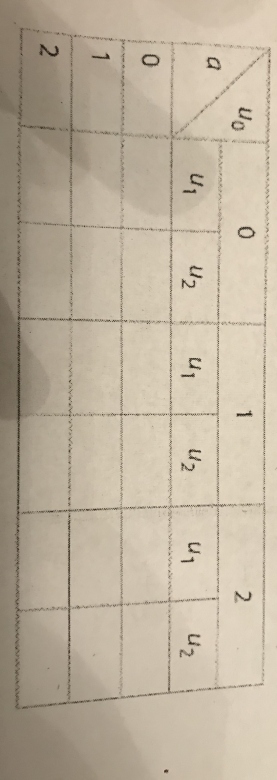Je cite :

Merci beaucoup ! Mais si p ne vaut pas 2 donc p est impair . On a donc p+4r avec p impair . Donc p+4r impair comme p est impair et 4r pair . Mais comment je peux prouver qu'il est composé ?

salut

?

Bonjour à tous,
@Matoutiques,

Pour 2)a)
1er terme : u₀ = 3
2nd terme : u₁ = 3+r avec r entier naturel non nul.
Il suffit d'écrire le 4ème termeet de constater qu'il n'est pas premier.

Pour 2)b), c'est pratiquement pareil.

Pour la question 2, on va déjà simplement recopier la question :
On s'intéresse aux suites arithmétiques  qui commencent par p=3
Donc dees suites du type (3, 3+r, 3+2r, 3+3r , 3+4r ... ...)

Parmi les nombres 3+r, 3+2r, 3+3r, 3+4r, 3+5r ..., est-ce qu'il y en a 1 pour lequel on pourrait affirmer : ce nombre est composé, quelle que soit la valeur de r ?

Tout à fait, 3+3r est un multiple de 3.
J'ai l'impression qu'on tient la réponse à la question suivante.

@Matoutiques,
Inutile de mettre des placards de citations. Ça encombre inutilement.

@ty59847´
Mais du coup pour la 2)a) pourquoi il demande pour le 4 eme terme ? Et non le 3ème ?

Oh oui car peu importe le nombre p premier il finira par y avoir un nombre non premier dans la suite
Par exemple si on prend 11 bah au 11eme terme de la suite on aura 11+11r donc ça sera plus premier
C'est ça ?

Oui, mais ce sera le 12ème terme.
11 sera le 1er, 11+r le second, 11+2r le 3ème, 11+3r le 4ème, ...

Oh donc c'est pour ça qu'à la question 2 il demande le 4 eme terme
Car le premier est
3
Le deuxième
3+r
Le troisième
3+2r
Et le quatrième
3+3r donc composé car multiple de 3 ?

Et donc pour la 2)b on peut dire que le (p+1)eme terme d'une suite est un multiple de p donc il ne peut pas y avoir une suite uniquement composé de nombres premiers ?


Pour la 3 : je n'y arrive pas car plus on prend un grand nombre premier en point de départ  au plus la suite sera grande non ? R on peut toujours prendre un nombre premier plus grand en départ comme l'ensemble des nombres premiers et infini

2)a et b) : D'accord.

Ensuite, tu parles de 3) ou de 2)c) ou de 2)d) ?

Oh je voulais dire 2c)

L'énoncé de la question 2c) :
Soit une suite arithmétique de premier terme p premier.
Quel est le nombre maximum de nombres premiers en progression arithmétique pour une telle suite ?
La question n'est pas très bien posée.

Il faut généraliser ce que tu as écrit avec p =11.

Ah oui en effet je n'avais pas compris la question comme ça

Donc le nombre maximum de nombres premiers en progression arithmétique d'une t'elle suite est (p+1) nombres ?

On demande la longueur maximum de cette suite arithmétique. Dans le 1er cas, quand n valait 3, tu avais trouvé combien ?

Tu sembles dire qu'on peut trouver (p+1) nombres premiers.
Regarde ce que ça donne pour le cas p=3 ou p=11.

Doublée

Pour 3 j'en avais trouvé  3 et pour 11 j'en a vais trouvé 11. J'ai parlé trop vite (c'est vraiment des erreurs bêtes ça en plus). Donc c'est la p+1 mais p ?

*c'est pas

En commençant par p, on aura effectivement au mieux une suite de p nombres premiers en progression arithmétique.
Au mieux.
Et oui, c'est vraiment des erreurs bêtes. Il faut réfléchir avant d'écrire. Même si tu écris sur un forum et que des gens vont corriger tes étourderies, il faut éviter ces étourderies. Sinon, quand on ne sera pas là pour te tenir par la main, tu feras comment ?

Oui je sais  desoleee ...

Pour la d j'en ai trouvé une ca c'était simple
Pour la e j'ai commencé à écrire que
Un= p+nr
J'ai écris que p est premier donc p>0

Ainsi Un=p+nr> nr>=n

Pour la 3)a)
J'ai mis oui mais seulement une suite de deux termes (est ce suffisant pour être qualifié de suites )
C'est la suite de premier terme 2 et de raison 5 (donc la suite c'est 2 7)

Mais pour la 2)e)
Il faut donc que la raison soit positifs donc ? Car sinon ce n'est pas vrai par exemple prenons une progression arithmétique de premier terme 5 et de raison -3

U0= 5
U1= 2
U2 = -1


Il y a 3 nombres mais ils ne sont pas tous supérieurs ou égaux à 3

Pour la question d)  peux-tu donner la suite que tu as trouvée.
Pour la question e), recopie la question. Reformule la question, avec d'autres mots ou d'autres tournures de phrase.
Pour la 3a), tu as très bien répondu... recopie ce que tu as mis ici : ta réponse , et tes réserves, parce qu'une suite arithmétique qui comporte uniquement 2 termes, c'est effectivment un peu une arnaque.

Pour la e), " ils sont tous supérieurs ou égaux à N". Tu n'as démontré que pour le dernier.
La question est encore mal posée. Il est sous entendu que les termes sont premiers.

@ty59847,
Moi aussi, je suis curieuse de voir cette suite de 10 premiers

La raison doit être un nombre positif. Ce n'est pas une obligation en général, mais ici, c'est clair, l'auteur de l'exercice ne veut que des suites avec une raison strictement positive.

Sinon, si on veut s'amuser, on peut dire que la suite de premier terme 3 et de raison 0 contient une infinité de nombres tous premiers. Et donc, tout ce que tu as fait depuis le début serait faux.

@Matoutiques,
Pour insérer une image, utilise le bouton "Img" sous la zone de saisie.
Cadre bien sur le tableau. Pas de texte autour si possible.
Utilise le bouton "Aperçu" avant de poster pour vérifier que l'image est correcte et dans le bon sens.

@ty59847,
Oui, l'énoncé manque souvent de précision.
Le mot "maximum" dans la question 2)c) ne me semble pas approprié par exemple.
On pourrait répondre 36p

En fait c'était simple car je n'avais pas bien lu . Sauf qu'après avoir posté le message j'ai vu que c'était avec 10 entiers.

J'en cherche donc une depuis 30 minutes . J'ai aussi regardé sur internet et j'ai appris l'existence du théorème de Green tao. J'ai aussi lu qu'une suite de 10 nombres existait (même une de 26 !) mais c'est avec nombres à 93 chiffres ! Donc ce n'est pas dans la liste de nombres premiers qu'on a ...
Je vais envoyer un message à mon professeur.


Pour la e
Donc dans la question il est sous entendu que 1- les termes sont premiers
2- la raison est strictement supérieur à 0 et du coup elle doit aussi doit être un nombre entier ?

Apparement, tu cherches une suite de 10 nombres premiers, en progression arithmétique.  Soit. Si ça t'amuse.  Mais ce n'est pas demandé dans l'exercice.

Oui, la raison doit être un nombre entier. Bien sûr. Les termes de la suite doivent être des nombres entiers, donc la raison doit être un nombre entier.

Ce que tu écris est si surprenant que je me demande si tu travailles toujours sur le même exercice, ou sur autre chose.

Je dis sûrement des bêtises mais pour la e
J'ai pense à dire que
Dans une suite de progression arithmétique de nombres premiers
Si on prend  pour premier terme p premier
Le nombre maximum de nombres premiers en progression arithmétique était p

Donc ça va de
U0= p
A
U(p-1)=p+ pr

Il y a N =  p termes

Or Uo= p>= p
De plus cette progression est croissant car la raison est strictement positive donc tous les termes sont >ou égaux à p ?

Ce n'est pas ce que la question 2)d) demande  ? Une suite de 10 entiers  premiers en progression arithmétique ?

Si :

Ah oui, la question 2d.
Mais comme tu disais en début d'après-midi que tu avais trouvé cette liste, je ne pensais pas que tu étais revenu sur cette question.
A priori, pour t'aider, on te donne une liste avec tous les nombres premiers entre 2 et ... je ne sais pas combien.  Tu peux nous éclairer là dessus ?

Pour la question 2e), je pense que tu as à peu près la réponse. D'après moi, dans la réponse il faut rappeler le résultat de la question 2c, et il faut dire que la question 2c, ou la question 2e, c'est exactement la même question, mais présentée de façon différente.

Justement le problème c'est qu'on a pas cette liste le prof nous a juste donné ça comme ça ...
D'accord merci !
Du coup là je suis à la 3) b)
Je ne sais pas trop comment commencer ...

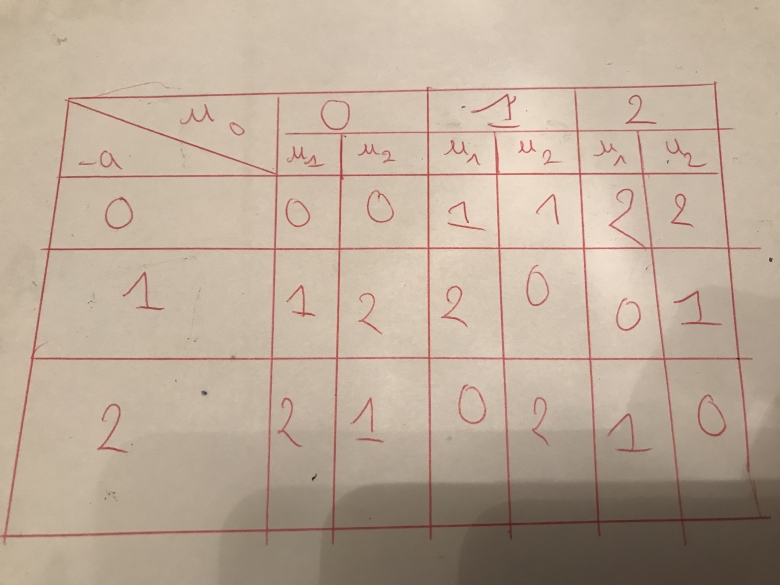
Par contre j'ai fais le tableau je vais vous l'envoyer

Voilà

Et j'ai mis

Poster le tableau vide, ça n'a pas beaucoup d'intérêt.  On avait deviné que c'était un quadrillage avec des lignes et des colonnes ! Ce qu'il faudrait, c'est que tu postes le tableau rempli, à ta façon.
Encore une fois, RECOPIE la question ; reformule la question.  On te demande de mettre quoi dans ce tableau ?
Dès que tu auras compris la question... tu auras la réponse.  Est-ce qu'il y a des mots compliqués, ou des notions compliquées dans la question ?

Ok , le tableau est correct.

D'accord , merci beaucoup !

Du coup pour 3 b) est ce que vous auriez une piste pour savoir comment je pourrais  commmencer ?


Aussi pour les questions en dessous du tableau j'ai mis que la plus petite valeur de u0 est 2
Et pour qu'est ce qu'on peut dire de la raison a je ne sais pas quoi dire
Appart qu'elle doit être supérieur à deux (et impair comme on l'a vu à la question juste avant le tableau ) car sinon u0 u1 et U2 ne sont pas premiers

Je vais attendre quelques minutes avant de te répondre. Normalement, dans 10 minutes, tu auras fini l'exercice sans la moindre aide.
Alors que si tu passes ton temps à taper tes questions et à attendre des indices, ça va prendre encore 3 heures.

J'ai continué à réfléchir sur cet exo
Pour la 3 b
J'ai mis sur mon brouillon que si il y a au moins 3 termes c'est qu'il Existe
U2= p+2r
J'ai mis que p était premier et impair (il ne peut pas valoir 2 car si p= 2 il n'y a que deux termes comme on l'a déjà prouvé en partie 1 )

Donc comme c'est une progression arithmétique il faut que U2 soit premier
U2 peut être premier si il est impair
Donc si p+2r est impair donc si 2r est pair
Mais du coup je ne comprends pas pourquoi r ne peux pas être impair ?


Pour les questions en dessous du tableau j'ai laissé ce que j'avais is : à savoir que la plus petite valeur de U0 sachant que u0 ect sont premiers est u0 = 2
J'ai mis qu'on peut en déduire que soit a=0 mais ça n'a pas d'intérêt ou soit a est strictement supérieur à 0 car sinon u1 et U2 ne sont pas premiers


J'ai fais la 4)a
J'ai mis que les nombres premiers inférieur à 10 sont 2/3/5/7 et donc que la raison doit être un multiple de 2*3*5*7=210

Pour la b) je sais que je devrais sûrement le servir de la a car on retrouve 210
Mais je n'ai pas encore trouvé comment