Inscription / Connexion Nouveau Sujet
Dm sur les variations de fonction
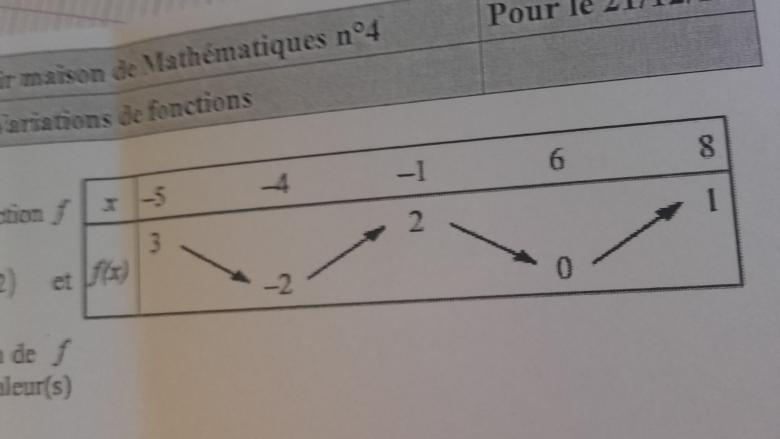
Voici le tableau de variation d'une fonction f définie sur [-5;8]
1) comparer si possible f (-3,2) et f(-3,19) justifier
2)donner sans justification le maximum de f sur [-2;8] et preciser ppur quelle(x) valeur(x) de x il est atteint.
3) donner dans justification le meilleure encadrement possible de f (x) si x E [-4;8] .
4) donner sans justification le nombre de solution de l'Équation f (x)= -1 sur [-5;8] . Préciser dans quel intervalle sz trouve la solution .
5) soit a E [-1;2]. Comparer si possible f (a) et f (a+1) justifier
Si il y a des gens qui réussissent merci de bien vouloir m'aider car je n'y arrive pas 😕
Bonjour
À quoi n'arrivez-vous pas ?
question 1 vous savez placer ces deux valeurs sur un des intervalles donnés
vous savez lire le sens de variation de la fonction et ce que cela induit
donc vous savez répondre à la première question
Bonjour,
Q1 ; -3,2 et -3,19 sont tous deux dans l'intervalle [-4; -1] dans lequel la fonction est .... (sens de variation lu sur le tableau)
Q2 : lire dans le tableau
etc
Merci grave à vous j'ai réussi à faire la 1 et 2 mais par contre je ne sais pas se qu'est un encadrement pour la 3 😕
Annuler
connectez vous