Niveau Reprise d'études

Droite véctorielle demande d'explication

Posté par
hbx360 21-03-22 à 09:31

Bonjour,

Je suis en train de voir la définition d'une droite vectorielle mais j'ai quelque doute sur la façon dont je comprends les choses pourriez-vous me dire si ceci est exacte :

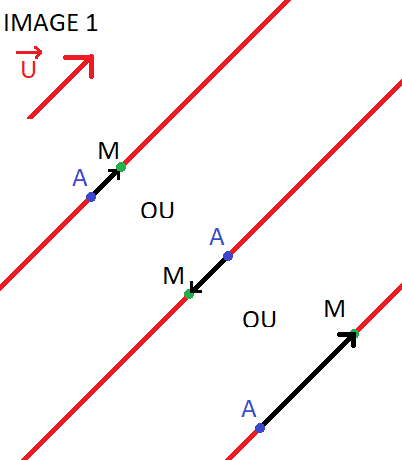
Image 1 : L'ensemble des points M appartenant à P (je suppose qu'ici que P c'est le plan) tel que $\vec{AM} et \vec{u}$ soit colinéaire, est une droite affine (je ne comprends pas ce que vient faire le mot affine ici à quoi correspond affine ?)  noté $D(A, \vec{u})$ (c'est la définition de la droite mais ou sont passés les points M (d'ailleurs je ne comprends pas comment on peut avoir plusieurs points M sur la même droite ? Dire l'ensemble des points M suggère qu'il y a plusieurs points M, mais peut-il y avoir plusieurs points M ? Je pensais que le point M était unique, qu'on ne pouvait qu'en avoir qu'un seul sur la droite ?).

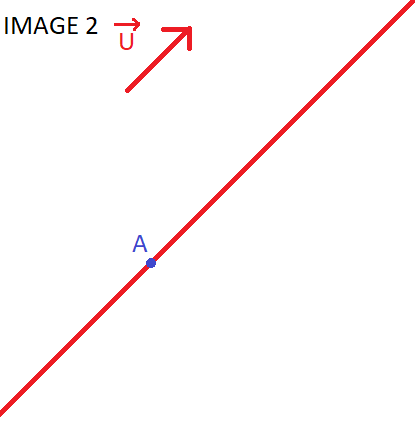
Image 2 : c'est la droite passant par A et dirigée par $\vec{u}$ .

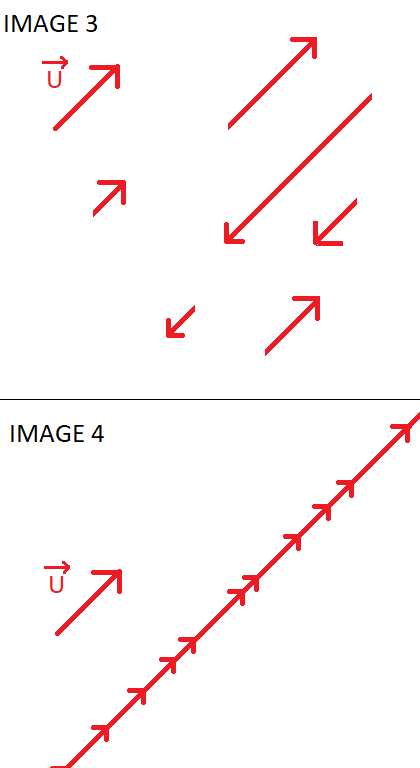
Image 3 : $\vec{D}$ c'est l'ensemble des vecteurs  colinéaire à   $\vec{u}$

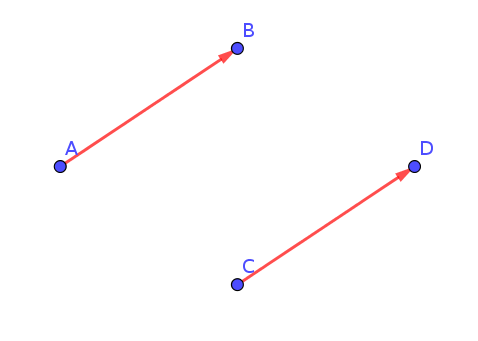
Image 4 : c'est la droite vectorielle engendré par   $\vec{u}$ ou ensemble des vecteurs de la droite D.

Je voudrai avoir une petite précision car j'ai l'impression que image 3 et 4 se contredises quand il est dit ensemble des vecteurs de la droite D est-ce que c'est uniquement les vecteurs qui sont effectivement sur la droite D ou bien cela inclue ce qui ne le sont pas comme sur l'image 3 ?

$Droite véctorielle demande d\'explication$

$Droite véctorielle demande d\'explication$

$Droite véctorielle demande d\'explication$

Posté par re : Droite véctorielle demande d'explication 21-03-22 à 10:00

Bonjour,

D'abord une réponse sur

Citation :
Dire l'ensemble des points M suggère qu'il y a plusieurs points M, mais peut-il y avoir plusieurs points M ? Je pensais que le point M était unique, qu'on ne pouvait qu'en avoir qu'un seul sur la droite ?

Le statut du "M" ici est celui d'une variable muette.
C'est le même que le statut de " $n$ " dans l'expression "l'ensemble des entiers $n$ tels que $n^2 +1$ soit divisible par 31".
C'est aussi le statut de "M" dans la phrase "Pour tout point $M$ de la médiatrice de $[AB]$ , on a $MA=MB$ ".

Ensuite, pour les vecteurs. As tu bien réalisé que les deux flèches sur les dessin ci-dessous représentent LE MÊME vecteur ?

$Droite véctorielle demande d\'explication$

Posté par re : Droite véctorielle demande d'explication 21-03-22 à 10:22

Paradoxalement, je vais t'expliquer la notion de droite vectorielle, puis la notion de droite affine.

Dans ta salle de classe, tu as plein de droites verticales. Le mot droite verticale, ça définit une droite vectorielle.
C'est une droite 'générique'. Et des droites verticales, il y en a plein dans ta classe, les 4 droites aux 4 angles de la salle, les 2 droites verticales au bord de la porte.
Chacune de ces 6 droites est une droite affine.

Une droite vectorielle, c'est une direction.
Et partant d'un point précis, dans une direction donnée, on peut tracer une droite, c'est une droite affine.
Jusque là, tu parlais de droite, sans vraiment préciser ...
Maintenant, on précise un peu le vocabulaire, et on introduit ce mot 'affine'.   Quand on parle de droite, pour parler de direction, on parle de droite vectorielle, et quand on parle de droite pour parler d'un ensemble de points, on parle de droite affine.

A noter qu'une droite vectorielle définit une direction ... mais c'est tout. Quand je parle de droite verticale, je ne dis pas si c'est de haut en bas ou de bas en haut.  Dans le dessin 4, toutes les flèches sont vers le haut, ça me plait moyennement... Disons que c'est pour l'esthétique qu'ils ont mis toutes les flèches dans le même sens.

Dans notre univers en 3D, Droite verticale, c'est une direction. Droite horizontale,ça ne suffit pas. Il faut préciser : droite horizontale parallèle au tableau, par exemple.

Maintenant, l'histoire des points M, comme s'il y avait plusieurs points M  etc.
C'est plus ou moins un abus de langage, c'est vrai.

P représente le Plan : oui.
A est un point qu'on a placé sur le plan. Il est là, il ne va pas bouger.
u est un vecteur, il définit une direction.

Ensuite je place un point M quelque part sur le plan. Et je vais faire plein de tentatives.
A chaque fois que le point M est tel que AM soit parallèle à u, je dessine une toute petite croix, sinon je ne dessine rien. Et je recommence plein de fois.
A chaque moment, j'ai un seul point M ... mais au bout de plein d'essais, j'ai dessiné une droite (une droite affine pour être précis).

Si on chipote beaucoup, on devrait écrire : L'ensemble des endroits où on peut placer M pour que AM soit parallèle à u, c'est la droite affine notée D(A,u)

Mais dans les faits, je n'ai jamais vu d'énoncé rédigé comme ça, tout le monde écrit la phrase que tu avais recopiée au début.

Et très souvent, les énoncés utilisent les lettres A, B, C, D  pour parler des points fixes. Et la lettre M pour parler d'un point qu'on cherche à placer dans le plan, et qui doit vérifier certaines contraintes.

Posté par re : Droite véctorielle demande d'explication 21-03-22 à 13:14

D'accord, donc pour construire la droite on a pas besoin que le vecteur colinéaire au vecteur u soit aligné les uns à la suite des autres et tous les vecteurs qui formeront la droite n'auront pas tous le même sens.

Posté par re : Droite véctorielle demande d'explication 21-03-22 à 13:55

Je recopie ta question :
D'accord, donc pour construire la droite (droite affine ou vectorielle ?)
on a pas besoin que le vecteur colinéaire au vecteur u soit aligné les uns à la suite des autres
Non, effectivement, si sur le dessin le vecteur u fait 1 cm de long, on peut très bien dessiner un vecteur parallèle à un mais plus court ou plus long, ou dans le sens opposé. Seule la direction compte.

Dans ton premier message, tu demandais des précisions de vocabulaire, mais tu écrivais des choses qui faisaient croire que tu avais presque compris. Là, c'est plus brouillon, moins encourageant.

Posté par re : Droite véctorielle demande d'explication 21-03-22 à 14:08

Un vecteur n'est pas porté par une droite fixe, ce n'est pas un glisseur (outil utilisé en physique pour représenter une force).

La droite dirigée par le vecteur non nul $\vec u$ passant par $A$ est l'ensemble des points $M=A+\lambda \vec{u}$ où $\lambda \in \R$ . Si $\lambda >0$ , alors $\lambda \vec{u}$ est de même sens que $\vec{u}$ et il est de sens opposé si $\lambda <0$ .

As-tu compris l'histoire du M unique ou pas qui te chiffonnait ?