Inscription / Connexion Nouveau Sujet
encore des fonctions avec cette fois ci leur variation
encore une fois je vient poster un autre problème de math 
inlassable le gaillard !
après celui la je m'arrête et j'aide les autres 
Soient trois fonctions 𝑓,𝑔,ℎ définies par
𝑓(𝑥)= 𝑥 ² −4,
𝑔(𝑥)= 2−𝑥/ 𝑥+1
,ℎ(𝑥)= 𝑥−2
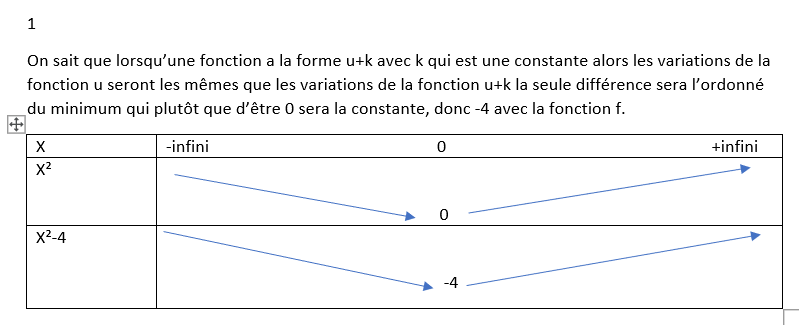
1. Dresser le tableau de variations de 𝑓.
2. Montrer que 𝑔(𝑥)=(3 /𝑥+1)−1.
Dresser le tableau de variations de 𝑔.
3. Montrer que la parabole de 𝑓, l'hyperbole de 𝑔 et la droite de ℎ sont concourantes en un point dont on déterminera les coordonnées.
le 1 fastoche, le a du 2 pareil mais le b du 2 
et le 3 j'imagine que on peut le faire facilement après avoir résolu le b du 2
voici mes réponses :
2
a
G(x)=3/x+1 -1
2-x/x+1=3/x+1 -1
2-x-3/x+1=-1
-1-x/x+1=-1
-1*1+x/x+1=-1
-1=-1
-1+1=0
et le 1 en image en bas
sinon pour le b du 2 j'ai réfléchi, je suis arrivé a la conclusion qu'il n'y avait que deux méthode pour dresser un tableau de variation
1 avec les dérivé on dérive un polynôme et paf !! c'est fait
et 2 avec les fonctions semblables aux fonctions de référence avec lesquels on s'amuse a faire des comparaisons
mais alors comment faire avec mon horrible g(x)= (3/x+1)-1
car ce n'est pas une fonction de référence caché du fait qu'il y a le petit plus 1 a coté du x et ce n'est pas un polynôme ca se voit
alors quel savante 
méthode doit je utiliser (sur qu'il y en a une autre que je n'ai pas vu et qui marche ici)
merci d'avance de vos réponses éclairés et illuminées
je ne comprends pas ta démonstration du 2a) ?
il te suffit de mettre 3/(x+1)−1 au même dénominateur et montré que tu retombes bien sur (2-x)/(x+1)
tu pouvais aussi partir de (2-x)/(x+1) et écrire que 2-x = -(x+1) + 3
mais partir de l'égalité des deux expressions à priori et montré que l'égalité est vrai pour tout x, c'est pas la méthode usuelle. En plus tu n'as pas vraiment justifié de cette façon.
Ton g(x)= 3/(x+1)−1 (mets bien les parenthèses 
) n'est pas horrible du tout
3/(x+1) est décroissant (fonction inverse) et donc 3/(x+1)−1 aussi.
ah! donc si j'ai bien compris on fait (3/x+1)- 1*x+1/1*x+1
ce qui donne 3-(x+1)/x+1 et donc 3-1-x/x+1 et donc 2-x/x+1
merci je n'avais pas vu cela
je ne savais pas que 2-x/x+1 était une fonction inverse, il me semblait que c'était que les fonctions avec 1/x et après ca le restait quand on multipliait ou divisait
es tu sur de toi que je peux dire que c'est une fonction inverse ?
Plus en détails : 1/x est la fonction inverse (connue comme décroissante)
donc 1/(x+1) aussi (on a fait une simple translation)
donc 3/(x+1) aussi (on a fait une homothétie)
donc 3/(x+1)−1 aussi (une nouvelle translation)
d'accord !! merci de m'expliquer, je pensais que sa changeait tout le fait que la modification intervienne au niveau du dénominateur 
alors voila mon résultat, néanmoins je crois que j'ai fait une erreur.
** image supprimée **
*** Modération > les scans de devoir ne sont pas autorisés ! * Si tu veux de l'aide, il faut recopier l'énoncé ***
Sujet ancien- ne plus donner ce lien-merci
Si tu ne mets pas de parenthèses, ce que tu écris n'a pas de sens.
la FAQ du forum
LaTeXLes scans sont interdits, si tu veux nous exposer des solutions il faut recopier les calculs.
Je suis obligé de supprimer l'image de ton dernier post.
aye le c** !!
désolé je l'ai fait sans réféchir
j'y ai même pas pensé (comme quoi je peut être très con parfois)
bon je reprend
2
a
G(x)=(3)/(x+1)-1
(2-x)/(x+1)=(3)/(x+1)-1
(2-x)/(x+1)=(3/x+1)-(1*x+1)/(1*x+1)
(2-x)/(x+1)=(3-1-x)/(x+1)
(2-x)/(x+1)=(2-x)/(x+1)
b
On sait que la fonction inverse est strictement décroissante sur R* donc on en déduit que g(x) est également strictement décroissante sur R*, en effet la fonction ne subit que quelques modification, la multiplication par 3, comme 3 est strictement positive il n'y aucun changement, l'addition et la soustraction par 1 qui ne change en aucun cas le sens de variation de la fonction.
et désolé mais je scanne quand même le tableau a la fin sinon c'est pas clair
et la suite avant de me faire expulser du forum
3
f(x)-h(x)=0
x²-4-x+2=0
x²-x-2=0
dans ce polynôme de second degré a=1 b=-1 et c=-2
delta =b²-4ac
=(-1)²-4*1*(-2)
=1+8
=9
Delta=9<0 donc l'équation a deux solutions x1 et x2
X1=(-b + racine de delta)/(2a)
=1+racine de (9)/(2*1)
=(4)/(2)
=2
X2=(-b-racine de delta)/(2a)
=(1-racine de 9)/(2*1)
=(-2)/(2)
=-1
Les solutions de cet équation sont donc 2 et -1.
h(x)-g(x)=0
(x-2)*(x+1)=x²+x-2x-2=x²-x-2
(x²-x-2)-(2-x)=0
X²-x-2-2+x=0
X²-4=0
X²=4
L'équation est de la forme x^n=b, avec n=2n=2 et b=4
n est pair b>0, l'équation admet donc deux solutions qui sont [2;−2]
on voit donc qu'il n'y a qu'une seule solution commune ou h(x) est a la fois égal a f(x) et g(x), on en conclu que cette solution est l'abscisse du point d'intersection des trois représentation graphiques des fonctions.
On calcule donc y en remplaçant x par la solution qui est 2, dans les fonctions.
F(x)=x²-4===f(2)=2²-4=4-4=0
H(x)=x-2===h(2)=2-2=0
G(x)=(2-x)/(x+1)===g(2)=(2-2)/(2+1)=(0)/(3)=0
Le point d'intersection des représentations graphiques des trois droites a donc pour coordonnées (2 ;0)
comme ca si on me vire au moins je fini en beauté
comme ca si on me vire au moins je fini en beauté
mais non, on est pas si méchant !
Tes calculs ont l'air justes. Vérifier graphiquement avec un logicien de géométrie est toujours une bonne idée.
Annuler
connectez vous