Inscription / Connexion Nouveau Sujet
Ensemble de points
Salut!
Le plan complexe est rapporté à un repère orthonormé (O,u,v). on considère l'application f qui au point M d'affixe z fait correspondre le point M' d'affixe z' tel que :
z' = ((3+4i)/5)z barre + (1-2i)/5
1) On note x , x' , y et y' les parties réelles et imaginaires de z et z'.
Démontrer que :
x' = (3x+4y+1)/5
y' = (4x-3y-2)/5
Là je n'ai eu aucun problème , j'ai juste remplacer z et z' par leur expression en fonction de x et fait une identification (partoe réel - partie imaginaire)
2) Déterminer l'ensemble des points invariants par f .
Là j'ai posé f(M) = M => x=x' et y=y'
J'ai remplacé x' par x et y' par y dans leur expression et j'aboutis à :
x= 2y + 1/2
y = (1/2)x -1/4
Ma question est si est-ce que M d'affixe z = x + iy constitue l'ensemble des points invariants par f ?
Salut
Pour les points Invariants c'est très bien x=x' et y=y'
Donc
x= (3x+4y+1)/5
y= (4x-3y-2)/5
Tu résouds ce système 2 équations à 2 inconnues pour trouver x et y Et c'est tout
Bonjour,
Juste un petit complément :
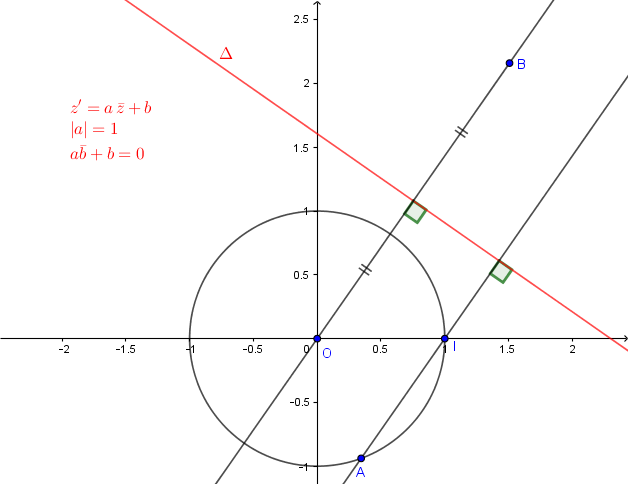
est l'écriture complexe d'une similitude indirecte.
Si , c'est un antidéplacement (réflexion ou symétrie glissée).
Si de plus , c'est une réflexion.
d'affixe
de module
est sur le cercle unité.
d'affixe
est alors sur la parallèle à
passant par
.
L'axe de la réflexion est la médiatrice de
.
Annuler
connectez vous