Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale ArithmétiqueTopics traitant de Arithmétique [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Ensemble de points

Posté par
matheux14 06-09-20 à 14:44

Bonjour ,

Merci d'avance.

ABC est un triangle équilatéral de centre O.

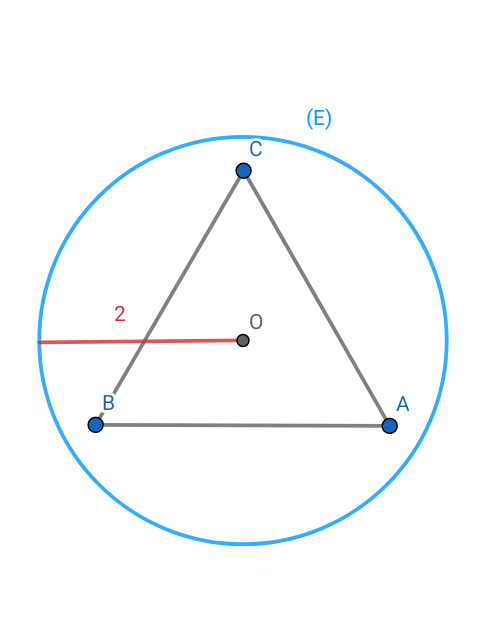
1) Déterminer et construire l'ensemble (E) des points M du plan tels que : ||\vec{MA}+\vec{MB}+\vec{MC}||=6.

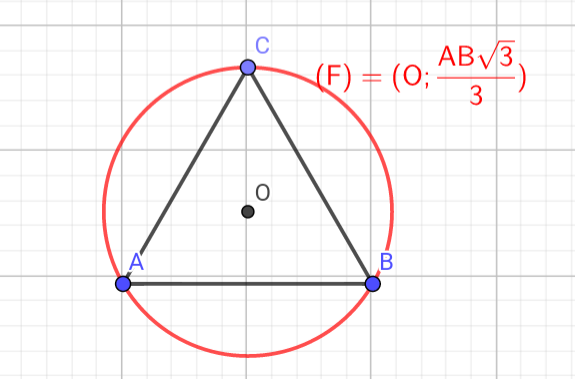
2) Déterminer et construire l'ensemble (F) des points M du plan tels que : ||\vec{MA}+\vec{MB}+\vec{MC}||=||2\vec{MA}-\vec{MB}-\vec{MC}||.

Réponses

1) On a : O le centre du triangle ABC.

D'où O=bar {(A,1) ; (B,1) ; (C,1)}

Donc \vec{MA}+\vec{MB}+\vec{MC}=3\vec{MG}

3||\vec{MG}||=6 \iff ||\vec{MG}||=2

MG = 2 , (E) est le cercle de centre O et de rayon 2.

Ensemble de points

2) ||\vec{MA}+\vec{MB}+\vec{MC}||=||2\vec{MA}-\vec{MB}-\vec{MC}||.

On a O=bar{(A,1) ;(B,1) ; (C,1)}

Soit G =bar {(A,2) ; (B,-1) ; (C,-1)}

\vec{MA}+\vec{MB}+\vec{MC}=2\vec{MA} -\vec{MB}-\vec{MC} \iff 3\vec{MO}=0\vec{MG} \iff \vec{MO}=\vec{0}.

MO=2 donc (F) est l'ensemble vide.

Posté par
matheux14re : Ensemble de points 06-09-20 à 14:46

MO=0 donc (F) est l'ensemble vide.

Posté par
heklare : Ensemble de points 06-09-20 à 14:54

Bonjour

Si vous appelez O le centre de gravité pourquoi ensuite utilisez-vous G  question 1

Question 2

2-1-1=0 donc pas de barycentre

Posté par
matheux14re : Ensemble de points 06-09-20 à 15:08

Oups c'est une erreur de frappe ..

Ah oui ,

2) ||\vec{MA}+\vec{MB}+\vec{MC}||=||2\vec{MA}-\vec{MB}-\vec{MC}|| \\ \iff ||-\vec{MA}+2\vec{MB}+2\vec{MC}||=0

Soit G =bar {(A,-1) ; (B,2) ; (C,2)}

||\vec{MA}+2\vec{MB}+2\vec{MC}||=0 \iff 3||\vec{MG}||=0

J'en déduis quoi pour (F) alors ?

Posté par
heklare : Ensemble de points 06-09-20 à 15:24

La norme d'une somme n'est pas la somme des normes   revoir votre équivalence

on appelle A' le milieu de [BC]  donc \vec{MB}+\vec{MC}=2\vec{MA'}

d'où 2\vec{MA}-2\vec{MA'}=

Posté par
matheux14re : Ensemble de points 06-09-20 à 15:28

Ok ,

Citation :
on appelle A' le milieu de [BC]  donc \vec{MB}+\vec{MC}=2\vec{MA'}

d'où 2\vec{MA}-2\vec{MA'}={\red{\vec{0}}


Donc (F) est la médiatrice du segment [BC].

Posté par
heklare : Ensemble de points 06-09-20 à 15:33

Non ce serait vrai si A=A'

Ce n'est pas le cas l'un est un sommet l'autre le milieu du côté opposé

\vec{MA}+\vec{A'M}=

Posté par
matheux14re : Ensemble de points 06-09-20 à 15:47

\vec{A'A}

Posté par
heklare : Ensemble de points 06-09-20 à 15:48

Oui

\|\vec{A'A}\|=

Posté par
matheux14re : Ensemble de points 06-09-20 à 15:50

\dfrac{AB²\sqrt{3}}{2}

Posté par
heklare : Ensemble de points 06-09-20 à 16:02

Non  pourquoi AB^2

La hauteur dans un triangle équilatéral de côté a est \dfrac{a\sqrt{3}}{2}

Posté par
matheux14re : Ensemble de points 06-09-20 à 16:08

Erreur de frappe , désolé

Posté par
matheux14re : Ensemble de points 06-09-20 à 16:08

matheux14 @ 06-09-2020 à 15:50

\dfrac{AB\sqrt{3}}{2}

Posté par
heklare : Ensemble de points 06-09-20 à 16:11

Il faudrait conclure  pour l'instant on en est à

3\|\vec{MO}\|=AB\sqrt{3}

Posté par
matheux14re : Ensemble de points 06-09-20 à 16:18

D'accord , ||\vec{MO}||=\dfrac{AB\sqrt{3}}{3}

(F) est donc un cercle passant par O et de rayon \dfrac{AB\sqrt{3}}{3}

Posté par
heklare : Ensemble de points 06-09-20 à 16:30

Il faudrait sans doute faire plus attention  il ne passe pas par O  puisque O est le centre du cercle

Posté par
matheux14re : Ensemble de points 06-09-20 à 16:36

Ah ok ,

(F) est donc le cercle de centre O et de rayon \dfrac{AB\sqrt{3}}{3}

Posté par
heklare : Ensemble de points 06-09-20 à 16:48

Bien sûr

Posté par
matheux14re : Ensemble de points 06-09-20 à 17:30

Voilà le schéma :

Ensemble de points

Posté par
heklare : Ensemble de points 06-09-20 à 17:54

Oui  Pouvez-vous prouver que c'est bien le cercle circonscrit au triangle ABC ?

Posté par
matheux14re : Ensemble de points 06-09-20 à 18:05

Non , je n'y arrive pas ..

Posté par
heklare : Ensemble de points 06-09-20 à 18:13

[AA'] est une médiane   le centre de gravité est situé au 2/3 du sommet

On a donc
AO=\dfrac{2}{3} AA' = \dfrac{2}{3}\times AB\dfrac{\sqrt{3}}{2}=AB\dfrac{\sqrt{3}}{3}

Posté par
matheux14re : Ensemble de points 06-09-20 à 18:36

Ah ok , merci

Pour la rédaction :

||\vec{MA}+\vec{MB}+\vec{MC}||=||2\vec{MA}-\vec{MB}-\vec{MC}||

Donc \vec{MA}+\vec{MB}+\vec{MC}=2\vec{MA}-\vec{MB}-\vec{MC}

Comme 2-1-1=0 , le 2e membre de cette égalité n'a pas de barycentre.

Posons A' le milieu de [BC].

On a donc \vec{MB}+\vec{MC}=2\vec{MA'}

==> 2\vec{MA}-2\vec{MA'}=3\vec{MO} \iff 2(\vec{A'M}+\vec{MA})=3\vec{MO} \iff 2\vec{A'A}=3\vec{MO}.

Or A'A=\dfrac{AB\sqrt{3}}{2} car (A'A) est une médiane du triangle ABC.

D'où 2A'A=AB\sqrt{3}

Donc 3MO=AB\sqrt{3} \iff MO=\dfrac{AB\sqrt{3}}{3}

Posté par
heklare : Ensemble de points 06-09-20 à 18:52

Donc \vec{MA}+\vec{MB}+\vec{MC}=2\vec{MA}-\vec{MB}-\vec{MC}
est une proposition fausse

l'égalité en norme ne veut pas dire l'égalité  en vecteur

2 On a montré  la question précédente que \| \vec{MA}+\vec{MB}+\vec{MC}\|=3\|\vec{MO}\|

Considérons A' le milieu de [BC]. Il en résulte que \vec{MB}+\vec{MC}=2\vec{MA'}

On a alors 2\vec{MA}-\vec{MB}-\vec{MC}=2\vec{MA}-2\vec{MA'} =2\vec{A'A}

L'égalité   \|\vec{MA}+\vec{MB}+\vec{MC}\|=\|2\vec{MA}-\vec{MB}-\vec{MC}\|

peut alors s'écrire 3\|\vec{MO}\|=2\|\vec{A'A}\|

Citation :
car (A'A) est une médiane du triangle ABC.
  [AA'] est une hauteur   c'est la longueur d'une hauteur que l'on connaît dans un triangle équilatéral  ensuite les autres

Posté par
matheux14re : Ensemble de points 06-09-20 à 19:05

Citation :
Considérons A' le milieu de [BC]. Il en résulte que \vec{MB}+\vec{MC}=2\vec{MA'}
Cette partie me fatigue un peu ..

Posté par
heklare : Ensemble de points 06-09-20 à 19:15

Vous voulez le détail  ?

\vec{MB}+\vec{MC}=\vec{MA'}+\vec{A'B}+\vec{MA'}+\vec{A'C}=2\vec{MA'} +\vec{A'B}+\vec{A'C}

or \vec{A'B}+\vec{A'C} =\vec{0}  puisque A' est le milieu de [BC]

Donc \vec{MB}+\vec{MC}= 2\vec{MA'} c'est parfois un résultat du cours tellement il sert

Posté par
matheux14re : Ensemble de points 06-09-20 à 19:18

Oui , j'y est pensé , mais j'ai douté ..

Merci et bonne soirée !

Posté par
heklare : Ensemble de points 06-09-20 à 19:20

De rien  
Bon courage pour la rédaction
Bonne soirée


Rechercher
Menu
Espace membre
10 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !