Inscription / Connexion Nouveau Sujet
Équation en seconde
Bonjour,
Je suis jeune professeur et je projette de donner à mes bons éléments de 2nd GT un exercice plus difficile pour les occuper en classes. Seul problème: je bloque sur l'exercice à résoudre (vous pouvez envoyer vos tomates et vos ?ufs pourris).
L'exercice est le suivant:
Le triangle ABC rectangle isocèle en B est tel que AB = BC = 4cm. On note M le point de [AB] tel que AM = x avec . On place les points P et Q respectivement sur [BC] et sur [AC] tels que le quadrilatère MBPQ soit un rectangle.
Partie A:
1) Exprimer MB en fonction de x. MB=4-x
2) Pour quelle(s) valeur(s) de x le rectangle MBPQ est-il un carré ? On détermine MP grâce à Thalès => MP = x, et on souhaite avoir MB = MP, donc x=2
3) Montrer que l'aire S(x), en cm², du rectangle MBPQ est égale à: x(4-x). Aire du rectangle = L * l = MB * MP = x(4-x)
4) Tracer une représentation graphique de S
Partie B:
1) Donner les dimensions du rectangle MBPQ, lorsqu'ils existent, ayant pour aire 2, 4 et 5cm². Et c'est là que je bloque !!
On souhaite en réalité avoir x(4-x)=2 pour commencer, mais j'ai beau tourner et retourner le problème dans tous les sens, pas moyen de résoudre cette équation (avec les connaissances de seconde bien sûr ... ça suffit les tomates et les ?ufs pourris).
Peut-être suis-je passer à côté de quelque chose, je trouverai dommage de devoir m'en remettre à la représentation graphique.
J'en appelle à la communauté pour essayer de résoudre le problème au niveau seconde, HELP !
Belle soirée à tous,
Amicalement,
LM
Bonjour,
1ère idée :
tu peux demander une lecture graphique et faire trouver des valeurs approchées à partir du graphique de la question précédente ou sur la calculatrice graphique
2ème idée même si ça me parait un peu compliqué : utiliser le début d'une égalité remarquable
x(4-x)=2
4x-x²=2
x²-4x+2=0
(x-2)²-4+2=0
(x-2)²-2=0
soit on factorise la différence de deux carrés
soit on passe par
(x-2)² = 2
deux nbres ayant le même carré sont égaux ou opposés
voilà Ludo ce que mon ancienneté te lègue !
Bonjour,
Au lieu de x = AM, tu peux définir dès le début comme inconnue x = IM où I est le milieu de AB. Cela ne change pas la difficulté de la partie A.
Du coup la méchante équation du second degré de la partie B devient (2-x)(2+x) = 2 (ou 4, ou 5...)
Mais il faut soit imposer M à droite de I, soit discuter le fait qu'il y a deux rectangles de même surface possibles...
Bruno
Bonjour,
sauf erreur de ma part, on étudie la forme canonique de ax²+bx+c en 2de donc la méthode préconisée par garnouille me paraît OK.
arrivé à (x-2)²-2=0 on résous en utilisant l'identité remarquable a²-b² et ensuite produit nul
4) Tracer une représentation graphique de S
Partie B:
1) Donner les dimensions du rectangle MBPQ, lorsqu'ils existent, ayant pour aire 2, 4 et 5cm². Et c'est là que je bloque !!
je trouverai dommage de devoir m'en remettre à la représentation graphique.
Plutôt que de vouloir mettre en oeuvre des méthodes qui relèvent du programme de 1ère, pourquoi ne pas utiliser proprement une méthode graphique puisque la courbe a été tracée. Cette méthode n'a rien de déshonorant ; pour des choses plus compliquées, elle est parfois la seule disponible...

Tu peux aussi compléter en faisant utiliser le MODE TABleau des calculatrices de tes élèves. Cela pourra leur être utile de comprendre cette approche dans la perspective de l'application du calcul d'une valeur approchée par encadrement (TVI)... dans les classes ultérieures.
on peut même en remettre une couche dans le style "graphique" avec GEOGEBRA et en "zoomant' .....
Bon courage à toi et j'espère que nul n'osera t(nous)'envoyer des tomates 
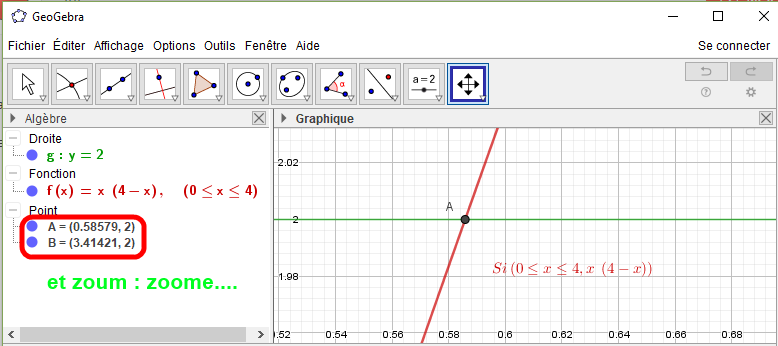
Bonjour et merci pour ces rapides retours,
La forme canonique d'un polynôme du second degré est effectivement au programme, mais je n'ai pas encore aborder ce point de l'année avec eux. Vu comme l'exercice est construit, je pense effectivement que la meilleure réponse est une lecture graphique. Dans la suite de l'exercice, ils nous guident pour pouvoir donner algébriquement le ou les antécédents de 3 par la fonction S.
Pour ce qui est de définir x = IM cela semble compliqué à mettre en place. Dans un sens l'exercice impose AM= x, et dans l'autre effectivement ça amène à plusieurs discussions quant à la position de M sur [AB] vis à vis de I.
Merci à tous.
AH ... je ferais attention en faisant mon cours. NE PAS REGARDER SESAMATHS.
merci de cette précision !
NE PAS REGARDER SESAMATH
Mais si , mais si.... c'est une bonne source documentaire

mais toujours être attentif à l'évolution des programmes et à l'interprétation pas toujours rigoureuse qui en est faite ici ou là

salut
1) Donner les dimensions du rectangle MBPQ, lorsqu'ils existent, ayant pour aire 2, 4 et 5cm². Et c'est là que je bloque !!
on peut évidemment résoudre le pb avec une calculatrice : résoudre l'équation f(x) = k est un attendu du programme ou avec geogebra ...
on peut aussi poser une question préliminaire :
montrer que x(4 - x) = 4 - (x - 2)^2
...