Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
espace de Hilbert séparable et base orthonormale
Posté par romu
Bonsoir,
voilà un théorème dont je ne vois pas commencer la démo:
Citation :
Théorème: (Représentation suivant une base orthonormale en dimension infinie)
Soit)) un
un 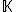 -espace de Hilbert séparable de dimension infinie et soit
-espace de Hilbert séparable de dimension infinie et soit  la norme associée.
la norme associée.
Soit_{k\in \mathbb{N}}) une base orthonormale et soit pour tout entier
une base orthonormale et soit pour tout entier 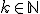 la forme linéaire
la forme linéaire 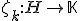 avec
avec
=(x|v_k)) pour tout
pour tout 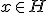 .
.
Alors la forme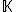 -linéaire
-linéaire 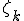 est continue et pour tous
est continue et pour tous 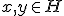 :
:
(a) la série vectoriellev_k) converge dans
converge dans 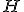 et
et v_k) ;
;
(b) la série numérique|^2) converge dans
converge dans 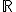 et
et |^2) , égalité dite de Parseval;
, égalité dite de Parseval;
(c) la série numérique\overline{\zeta_k(y)}) converge dans
converge dans 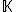 et
et =\Bigsum_{k=0}^{\infty} \zeta_k(x)\overline{\zeta_k(y)}) .
.
Théorème: (Représentation suivant une base orthonormale en dimension infinie)
Soit
Soit
Alors la forme
(a) la série vectorielle
(b) la série numérique
(c) la série numérique
Pour la (a), déjà, je ne vois pas comment faire (sachant qu'on a montré justement avant un théorème analogue pour le cas de la dimension finie).

Merci pour votre aide.



 analyse en post-bac
analyse en post-bac