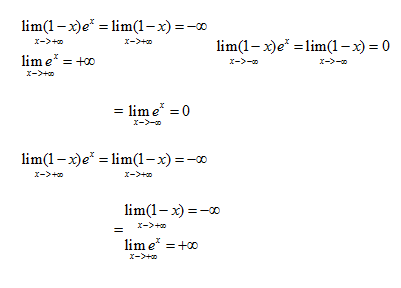Inscription / Connexion Nouveau Sujet
pour l'etude de signe j'ai modifié le tableau ci-dessous.
Ensuite je pense qu'il faut que je calcul les branches infinie pour lim (1-x)e^x quand x -> + = +-
= +- ?
?

Bis repetita (ce n'est pas des remarques seulement sur la forme pour t'embêter, tu perturbes le fonctionnement du forum)
du texte et des calculs et des formules ne doivent pas être une copie d'écran de Word mais du texte tapé ici
ou copié-collé depuis Word en tant que texte si ça te chante de passer par Word, mais pas en forme d'image
les images c'est exclusivement pour des figures et des "tableaux "compliqués" (si on ne sait pas les faire en LaTeX directement)
- les moteurs de recherche sur l'ile ne fonctionnent pas si le texte est planqué dans des images
- il est impossible de copier une partie du texte pour le citer etc.
- en plus une image est plus lourde dans les disques durs des serveurs de l'ile, mais bon, de nos jours on ne compte plus trop les Tera octets inutiles, le gaspi se loge partout
question 7 OK , mais rédaction pas finalisée (pas de conclusion formelle, que des calculs) et de toute façon inutilement lourde
s'arrêter à F '(0) = 0 suffisait !
question 8 : faux (il restait encore une autre erreur dans le tableau F(0) ne vaut pas 0, signalée par les carita)
question 9
F''(x) = -e^x -xe^x
peut on simplifier comme tu l'as fait ? certainement pas
le mieux qu'on puisse faire est de mettre e^x en facteur (et en plus ça sera comme d'hab pour résoudre une équation : "produit nul")
ensuite par définition le point d'inflexion sera lorsque F ''(x) s'annule en changeant de signe.
donc étudier le signe de F ''(x)
limites : pas très très lisible
je retiens :
ce qui nous a permis d'en déduire que (Ox) est asymptote horizontale (cf cours)
ces 2 limites doivent se retrouver sur le tableau de variation, tout simplement.
----
7) on a déjà corrigé cette question (tu l'as lu ?)
tu vois bien que tu as écrit que f(0) = 1 ? 
8) corrige l'expression de Yt générale
puis erreur de signe sur l'équation de la tangente en 1 (développement)
9) f ''(x) = - ex - xex exact
==> factorise ex
puis étudie le signe de cette dérivée seconde
regarde dans le cours la conclusion que tu peux en tirer
de mon côté c'est Internet qui recommence à merder avec toutes ces demandes de la part de la page du site vers Google, amazon, facebook etc etc sans parler de celles au serveur LaTeX (ni du chargement d'images inutiles  )
)
bref plusieurs minutes pour charger une page ... quand je ne suis pas obligé de l'interrompre au vol parce que dure vraiment trop longtemps.
bref répondra qui répondra ...
(je ne te reproche pas de mettre tes tableaux en image mais de mettre le texte et les calculs en image ...
ainsi dans to message d'avant il était impossible de copier-coller la formule F ''(x) = -e^x - x e^x pour la citer)
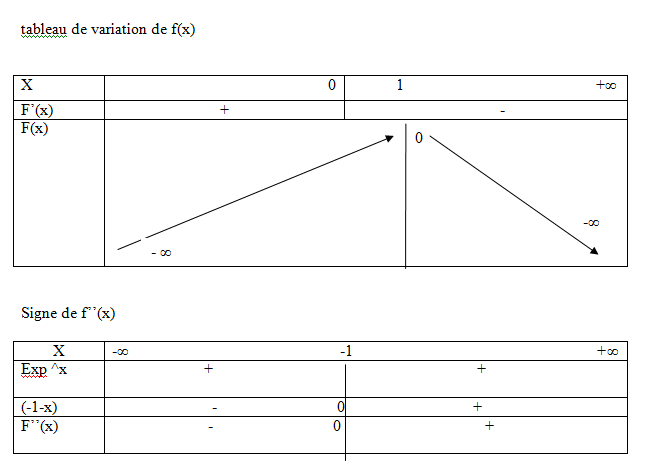
c'est toujours faux pour F(x)
(et même doublement faux car F(x) n'est pas croissante pour x entre 0 et 1 !!
tu corriges une erreur pour en ajouter une autre)
la limite de F(x) en -oo n'est pas -oo
la valeur de F(x) en x = 0 n'est pas 0
dans le tableau de F(x) la valeur de x = 1 n'a pas à figurer
évidement si parmi tous ces messages ici si tu choisis ceux où le calcul est faux au lieu de ceux où le calcul est juste tu n'y arriveras jamais !
relis le dernier message de carita qui te résume les bonnes valeurs des limites et de F(0)
ensuite pour ton tableau avec F ''(x) il est lui aussi faux (erreur de signes)
Gnyfer74, je veux pas embêter le monde...mais tu nous mets image sur image, pour des choses qui ne sont pas tolérées...et si je les supprime, on ne va plus rien comprendre...
je tolère le tableau de variations (bien que le site nous fasse ça très facilement avec ça :
(ce qui est entouré en rouge)
mais les limites et autres quand même, les images c'est un peu abuser
fais quelques tests rapides avec l'aide que j'ai entourée
oui, même mieux, avec ce que j'ai entouré
on visualise directement le rendu en allant des modifs
donc on voit en allant ce qu'il faut faire pour modifier....
c'est vrai ...
le moteur de rendu de l'éditeur LaTeX donnant un rendu identique ou presque (quelques effets de bord il me semble me souvenir) du moteur de rendu de l'ile elle même.
Gnyfer74, si tu permets.
je vois bien que tu galères !
ton acharnement à donner des réponses montre bien que tu veux y arriver,
mais tu donnes l'impression de répondre aux fléchettes, et surtout de ne pas bien t'organiser.
prends une feuille blanche, où tu notes tous tes résultats quand tu les as trouvés,
et avant de rédiger à l'écran, réfléchis avec crayon+papier.
et lis-tu bien tous nos messages ?
on n'a pas cette impression, car tu réitères des erreurs comme si tu n'avais pas lu
ou pas compris (demande si tu ne comprends pas telle ou telle réponse qui t'est faite!).
par exemple : je t'ai conseillé de tracer la courbe de f sur géogébra : l'as-tu fait ? j'ai des doutes ^^
si tu l'avais fait, l'allure de la courbe + les calculs de limites trouvées,
... sur le tableau de variation, il y a un moment que tu ne nous dirais plus que f(x) tend vers -inf lorsque x tend vers -inf !
--- fin du laïus
pour t'aider à avancer, je fais une petite récap pour le début, et je reviens.
en attendant, trace la courbe de la fonction et de la dérivée et confronte tout ça à ton tableau de variation 
Je suis désolée je patauge je comprends rien mais je vous assure que je lis tout vos messages et que j'essaie de comprendre !!! J'ai tracé la courbe sur GeoGebra et justement je vois bien que j'ai faux mais je ne comprends pas... Je fais tout ce que je peux... Et je vais l'exercer pour écrire avec latex c'est pas pour embêter le monde que je met des image c'était pour que sa soit plus lisible pour vous..''
f(x) = (1-x)ex
Df =  --- aucune valeur interdite (pas de double barres sur les tableaux !)
--- aucune valeur interdite (pas de double barres sur les tableaux !)
limites aux bornes :
--- lorsque x tend vers -
 , f(x) tend vers 0, donc se rapproche de l'axe des abscisses
, f(x) tend vers 0, donc se rapproche de l'axe des abscisses
d'après le cours, l'axe des abscisse y=0 est asymptote horizontale à Cf
étude de la variation :
* f '(x) = ... = -x ex
* f '(x) = 0  -x ex = 0
-x ex = 0  x = 0
x = 0
* étude du signe (si tu tiens à faire un tableau)
* tableau de variation ---- on y rassemble tous les éléments précédents, on n' 'invente' rien; on complète seulement avec l'image de 0, que l'on calcule --> f(0)=1
la fonction est croissante puis décroissante; son maximum est 1 et est atteint en x=0
un petit tracé géogébra ou calculette (pour vérifier)
on voit :
- que la dérivée s'annule en 0 (positive avant, négative après)
- que Cf est croissante puis décroissante (conformément au signe de la dérivée)
- que la courbe Cf se rapproche de + en + de (Ox) quand x tend vers -oo : ça confirme la limite trouvée.
- le sommet (0;1), conforme au tableau de variation.
est-ce que tout est bien clair ? as-tu des questions sur cette partie ?
Bonjour,
Merci carita pour ton résumé qui m'as bien aidé !!
Voila les questions sur les points où je bloque :
Est ce que tu peux me ré - expliqué pour les limites ?
Pour faire le calcul on fait bien la limite à chaque membre ?
Lim (1-x)e^x quand X tend vers -oo on fait bien lim (1-x) et lim de e^x ?
Idem pour + pour ? Peut-tu me détaillé tes calculs.
Lors de l'étude de la dérivée doit on toujours calculer f'(X) = 0 ?
et peux tu me détaillé ton calcul pour résoudre l'équation f'(x) = 0 ?
Merci
les limites oui, on calcule séparément les limites d'un produit
si les deux limites sont infinies, ou si l'une est finie et non nulle ou les deux finies il n'y a pas de problème pour calculer la limite qui est le produit des limites
par contre si on obtient une forme indéterminée 0*oo (ou bien oo/oo) il faut faire un calcul plus subtil
ainsi la limite :
(et pas 0)
et on a la forme indéterminée et la limite n'est pas le produit des limites.
il y faut plus de subtilité et faire intervenir des limite de cours
pour tout n (forme indéterminée
)
pour tout n (forme indéterminée
)
ainsi
et on fait la limite d'une somme (ou d'une différence ici)
(cours sur les limites d'expressions de la forme
et 0 - 0 n'est pas une forme indéterminée du tout
on a donc bien
etc.
on veut étudier le signe de la dérivée, et les fonction "en général" (si elles sont continues) changent de signe en s'annulant.
donc résoudre f '(x) = 0 est une étape généralement nécessaire pour l'étude du signe de f '(x)
résoudre une équation produit nul ??
un produit est nul si un de ses facteurs est nul
donc si x est nul (x = 0) ou si e^x est nul (jamais, e^x est toujours strictement > 0)
Merci, je pense avoir compris mais il me faut de l'entrainement ...
Pour la suite de mon ds, donc question 7 j'avais juste en trouvant y = 1 et pour la 8 je ne comprend pas la remarque de carita :
"8) corrige l'expression de Yt générale
puis erreur de signe sur l'équation de la tangente en 1 (développement) "
J'ai bien modifié mon erreur de signe et je trouve yt = -xe + e
Par contre que dois-je corrigé dans l'expression ?
Pour rappel , voilà ce que j'avais répondu :
de même, je reviens sur ta remarque, Mathfou :
"question 7 OK , mais rédaction pas finalisée (pas de conclusion formelle, que des calculs) et de toute façon inutilement lourde
s'arrêter à F '(0) = 0 suffisait ! "
Quelle rédaction dois-je faire ?
tu t'arrêtes à F'(0) = 0 puis tu dis :
"et donc le coefficient directeur de la tangente en le point d'abscisse 0 est 0, cette tangente est donc horizontale"
la question 7 était bien : (pfff incopiable pour cause d'image, faut retaper)
7) Montrer l'existence d'une [u]tangente horizontale au point A x=0[/u]
non ?
pas "calculer des équations sans répondre à la question"
c'est la question 8 qui demande l'équation d'une (autre) tangente.
et pour l'expression générale dans cette question 8, il s'agit de ça (erreur d'étourderie)
qui est faux
(d'ailleurs en remplaçant à la fin a par 1 tu n'écris pas (x+1) non? tu écris bien (x-1) !)
Arfff j''ai du mal à faire les tableaux avec Latex...désolé j'espère que sa ira.
Voici mon tableau de signe pour la question 9 , est-ce juste ?
ce tableau est tout aussi faux vu que tu l'as recopié d'un tableau faux précédent, en ajoutant la valeur x = 0 qui ne sert à rien.
(la même erreur de signe sur le signe de -1-x)
la convexité c'est le signe de la dérivée seconde
et les points d'inflexion sont les points où cette dérivée seconde s'annule en changeant de signe.
bonjour à tous
Gnyfer74, pour l'étude du signe de la dérivée seconde f '',
on procède comme pour celui de la dérivée f' : on commence par résoudre l'équation f ''(x) = 0
on trouve une seule racine : -1
sur la ligne des x du tableau de signe, cette racine soit figurer, et elle seule (pas 0 : que viendrait-il faire ici ?)
==> quand tu places les signes + ou - sur le tableau, pense à vérifier en donnant une valeur à x, prise "au hasard".
par ex, ligne (-1-x) :
si x=0, alors -1-x = -1 négatif --- et non pas + comme tu l'as écrit
si x= -2, alors -1-x = -1+2= 1 positif : tu vois bien que le signe - ne convient pas, tu comprends ?
ça doit te mettre la puce à l'oreille que tu as fait une erreur qq part.
tu peux aussi tracer la courbe de f '' : elle doit confirmer ton tableau de signes
(question : sais-tu conjecturer le signe d'après une courbe?)
---
pour la question 7)
oups, en effet on ne demande pas d'établir l'équation de la droite 
heureusement que mathafou est vigilant !
tu l'as relu ton tableau ?...
pour l'autre question :
qu'a-t-on trouvé quand on a résolu l'équation f ''(x) = 0 ... ?
pardon une erreur de frape et je n'ai pas vérifier ..
pour f''(x) en +oo le signe est - .
Par contre sauf erreur de ma part nous n'avons pas vu ensemble f''(x) = 0 ?
et oui, en résolvant f ''(x) = 0 
... donc pas besoin de calculer, on sait que f(-1) = 0
---
par ailleurs, contrôle sur ton calcul :
f ''(x) = ex (-1-x)
donc f ''(-1) = e-1 (-1-(-1)) = e-1 * ? = ?
Alors la je bloque, on est bien d'accord que f''(x) = 0 et f''(-1) ne sont pas les mêmes choses ?
f''(x)= 0 je suis d'accord, par contre pour f''(-1) moi je trouve f''(-1)= e^-1 (-1+1) = e^-1
et non pas f''(-1) = 0 ?!
je fatigue ! punaise des erreurs de concentration ! allez j'arrête pour aujourd'hui !
merci encore pour votre aide !
Bonjour à tous
je reviens vers vous concernant la question 9 et 10 de mon DS .
question 9
il s'agissait de déterminer les coordonnées du point d'inflexion c'est de F( X )et conclure sur la convexité de F.
donc j'en déduis que le point d'inflexion c = - 1 et j'en conclus que la courbe traverse sa tangente .
est-ce exact ?
de même la question 10 me demande de représenter la courbe représentative C de la fonction f ( X ) et de représenter également YT sur un traceur .
Quelqu'un sait-il comment faire sur geogebra j'ai tracé f(x) et f'( X ) mais je ne sais pas faire la tangente et la courbe merci
oui. on a déja dit que le point d'inflexion était le point de la courbe pour lequel la dérivée seconde s'annule en changeant de signe, c'est à dire le point d'abscisse -1.
le signe de la dérivée seconde donne la convexité de la courbe.
avant l'abscisse -1, F '' est positive, la concavité est vers le haut (courbe "qui rit")
après l'abscisse -1, F '' est < 0, la concavité est vers le bas (courbe "triste")
et en un point d'inflexion "par définition" la courbe traverse sa tangente !
Sur Géogebra tu as l'outil "tangente", direct à cliquer
tu sélectionnes l'outil (dans les droites diverses, parallèles, perpendiculaires etc)
tu cliques sur le point de la courbe, puis sur la courbe et c'est fait.
Bonjour,
Merci pour ton aide, j'y suis arrivée.
Pouvez-vous me confirmer que mes resultats sur les questions suivantes sont justes :
*Q11 : calculer analytiquement les coordonnées du point I le mileur du segment [AC]
J'ai donc poser la formule avec A(0;0) et C (0;-1) c'est qui nous donne I (0 ; -0.5)
*Q12 : calculer analytiquement la distance d entre Bet C
Avec la formule
et B (0;1) et C(0;-1)
J'ai trouver BC = 2
Par contre pour la question 13 : Calculer l'aire de a du domaine limité par la courbe (c), l'axe des abscisses et les droites d'équations x = -1 et x=1 (indication : Integrer par partie en posant u =x .
Je ne sais pas si j'ai bien compris voilà ce que j'ai fait :
Est-ce ça ? et comment le simplifier encore ?
merci
Mais tu n'as pas intégré xex !
Pour l'intégrer, tu peux faire une IPP en commençant comme indiqué dans l'énoncé.
q11, q12, trivial, OK
Q13
je ne vois pas le rapport qu'il y a entre la question et ce que tu as calculé
"la courbe" c'est bien .
et donc ce qu'on cherche à calculer c'est
je ne comprends pas l'indice de l'énoncé vu que
est immédiat à calculer vu que
est sa propre dérivée donc aussi sa propre primitive
l'autre morceau ne nécessite aucune intégration par partie vu que on a démontré jadis que la dérivée de est
et donc que la primitive de est
sans aucun calcul additionnel
donc au final
pour simplifier, une fois ça calculé correctement, c'est comme d'hab : une pomme plus une pomme = deux pommes (que ce soit des pommes ou des "e" (des oeufs ?  ) c'est pareil ...
) c'est pareil ...
et que par contre les pommes et les poires ne s'additionnent pas entre elles.
ton (vu que c'est faux) se simplifiait "trivialement" (pour un élève de 5ème) en
Bonjour Mathafou,
Merci encore pour ton aide,
du coup j'ai calculer l'intégration de
est-ce juste ?
Par contre est ce vraiment ce que le prof attend ? du coup je n'ai pas bien compris son indication non plus.
ce que le prof attend est dans la tête du prof.
vu qu'on cherche à calculer une intégrale sur je ne vois pas pourquoi on irait chercher midi à quatorze heures avec l'intégration par parties d'une autre fonction (surtout après l'étude de
qu'on a déja faite !!)
autant intégrer par parties directement !!
c'est à dire :
ici (directement pourquoi prendre le seul bout de l'indice farfelu de l'énoncé ??) et donc
et donc
ce qui donne
donc déja tu as une erreur de signe dans ton calcul d'intégrale
(que si ça se trouve c'est pire qu'une erreur de signe, c'est la compréhension même du calcul d'intégration ... va savoir)
ensuite calculer sérieusement les
et simplifier sérieusement (retour à la case collège)
ne pas se mélanger les pinceaux dans les signes : retrancher -1 c'est ajouter 1 et retrancher ce résultat c'est retrancher 1
si par contre on suit à la lettre l'indice de l'énoncé (c'est à dire si on complique volontairement la chose) on calcule :
(l'intégrale d'une différence est la différence des intégrales)
et là on intègre par partie le deuxième bout seul comme dit l'énoncé avec
mais ça ce n'est pas ce qu'on cherche !! ce n'est que le bout
ce qu'on cherche c'est
etc
si tu as un doute sur un résultat tu peux toujours faire ça avec Geogebra, (ou XCAS) tu verras bien la valeur numérique qu'il te donne ...
ça ne te dira pas comment l'obtenir, ça c'est du calcul théorique, mais au moins tu pourras en vérifier la valeur !!
f(x)=(1-x)e^x
S=Intégrale[f,-1,1]
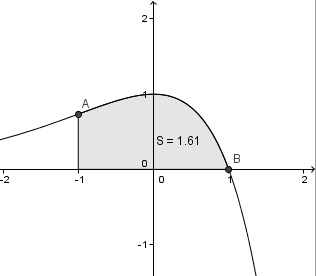
ton 3/e donnait 1.1036...
Bonjour,
Je suis désolé mais je bloque sur le calcul de l'integrale
ce qu'on cherche c'est
Moi je trouve
il n'y a rien de plus à expliquer : c'est du cours sur la signification de ce que veut dire "intégrer par parties"
les calculs ci dessus sont largement assez détaillés. je ne vois vraiment pas ce que je pourrais écrire de plus là dessus.
par contre ne pas savoir faire des simplifications correctement c'est grave
ma dernière expression donne :
les autres façons de calculer cette intégrale (intégration directe, ou intégration par parties de (1-x)e^x donnent bien entendu la même chose au final.
s'entrainer sur les signes de -(...-(-...))
Bonjour,
Je dois ensuite calculer la valeur moyenne, par contre j'ai un doute sur les primitives de et de
.
Pour , je dirais que la primitive est la même c'est à dire
par contre pour , je ne sais pas qu'elle formule appliquer.
merci
la primitive d'une constante a quelle qu'elle soit ???
que ce soit un truc qui s'écrit avec e ou  , une fraction ou n'importe quoi du moment que c'est une constante
, une fraction ou n'importe quoi du moment que c'est une constante
la primitive de a est ax + constante
mais pourquoi veux tu calculer une telle primitive ????
la valeur moyenne d'une fonction entre a et b est
c'est pas un truc en

est déja calculée !!
Ben je veux calculer ça car effectivement la valeur moyenne est bien la formule que tu cite , par contre dans l'énoncé le prof me donne une indication qui est : " utiliser le résultat de la question précédente " soit ...
bein oui !!
et ce "résultat de la question précédente" est bien le déja tout calculé.
tu as juste une simple division par 2 = 1-(-1) et c'est tout pour avoir
il n'y a aucun nouveau calcul d'intégrale à faire 
Bonjour,
ah ben oui .... j'avais mal compris la formule merci...
par contre désolé mais je bloque vraiment lorsqu'il s'agit de faire un calcul SIMPLE ALGEBRIQUE avec un exp.... je m'y perd...
Comment faire du coup le calcul de ???


e n'est pas "un exp"
e est un nombre comme 17, 25/3,  ou
ou  2
2
ce nombre est la valeur de la fonction e^x lorsque x vaut 1
il reste écrit e, comme  reste écrit
reste écrit  quand on veut des formules exactes et pas approchées
quand on veut des formules exactes et pas approchées
on peut "arranger" cette fraction "à étages" comme vu en 5ème / 4ème sur le calcul de fractions
pour simplifier ça en une fraction avec une seule barre de fraction
et ce quelle que soient la signification de a,b,c,d
que ce soit des nombres écrits numériquement, des nombres "symboliques" comme e ou  , voire même des expressions toute entières plus ou moins compliquées.
, voire même des expressions toute entières plus ou moins compliquées.