Inscription / Connexion Nouveau Sujet
Etude d'une fonction avec Arccos et Arcsin
Voilà je dois étudier cette fonction:
f(x) = Arccos
(1+sin(x))/2) - Arcsin(1+cos(x))/2.
Et je bloque d'emblée parce que je ne trouve pas son domaine de définition -_-.
Voilà, si quelqu'un pouvait simplement me débloquer, ça m'aiderai énormément 
Bonsoir.
On doit avoir compris entre -1 et 1
Ceci équivaut à :
0
Donc :
0
Je te laisse poursuivre.
Fais de même pour l'autre partie
1°) sous les racines pas de problème car : sont positifs
2°) pour les arccos et arcsin pas de problème non plus puisque je t'ai aidé à montrer que :
En conclusion ta fonction est définie sur IR.
Tu peux également remarquer qu'elle est 2
-périodique
Maintenant, calcule la dérivée. C'est un long travail, mai le résultat en vaut la peine. Je trouve :
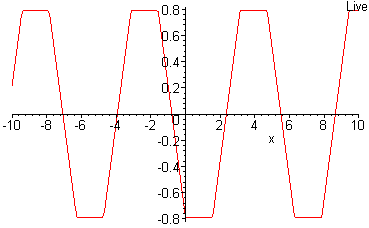
Suivant les signes de cos(x) et de sin(x), ce résultat devient : 0 ; 1 ; 0 ; -1
Cela signifie que f est constante ou affine, suivant les intervalles.
Pour la dérivée j'arrive à ça:
f(x)'= ( cos(x) / (4*((1+sin(x))/2)*((1-sin(x))/2) ) - ( sin(x) / (4*((1+cos(x))/2)*((1-cos(x))/2) )
Je vois pas comment arriver à ton résultat?
Merci d'avance 
Pas difficile :
fais le produit des racines. Tu te retrouveras avec des 1 - sin²x et des 1 - cos²x donc, des cos²x et des sin²x sous les racines.
Oula ouais merci beaucoup, les vacances m'ont pas fait que du bien moi, j'avais oublié qu'on pouvait multiplier les racines...
Pour démontrer la périodicité, j'applique la formule qui dit que T est la plus petite période si ça vérifie f(x+T)=f(x) ?
Ou alors comme j'ai sin(x) et cos(x) qui sont des fonctions périodiques je peux dire que c'est un composé de fonctions périodiques 2pi?
Tu peux utiliser la périodicité des fonctions sinus et cosinus.
Pour l'étude, aide toi de la représentation graphique de mon topic du 24-09-09 à 20:19
x
]O;
Annuler
connectez vous
analyse en post-bac