Inscription / Connexion Nouveau Sujet
Exercice avec geogebra
Salut voici un exercice que je n'arrive pas à faire (de A à Z) mais étant donner que je n'ai pas le temps d'eciuter les explications je vous demanderez exceptionnellement de me donner les solutions aux questions (je pourrez moi, de mon côté comprendre tout seul) merci de votre compréhension
Un rectangle abcd est tel que ab=8 et ad=10. AMIJ est un carre où M est un point de [AB] et J un point de [AD]. CKIH est un rectangle tel que K est le point de [CD] aligné avec M et I.
On se propose de déterminer les propositions de M pour lesquelles la somme des aires AMIJ et CKIH est égale à la moitié de l'aire du carré ABCD
1)Avec un logiciel de géométrie, créer un curseur a allant de 0 à 8 avec un incrément de 0,1.
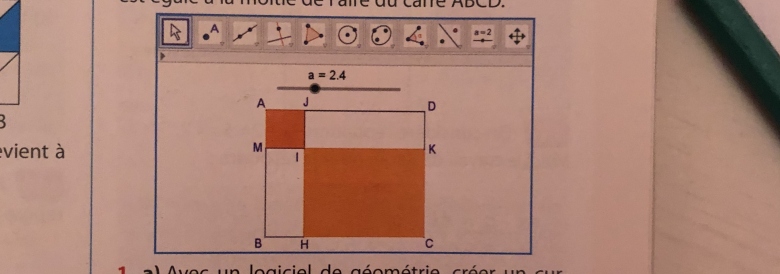
b)Réaliser la figure ci-dessus où M est le point de [AB] tel que AM=a. Afficher les aires de AMIJ, de CKIH et la somme S de ces deux aires.
c) Déplacer le curseur et conjecturer les positions de M solutions du problème
2)a)On note x la distance avec 0<(ou égal)x<(ou égale)8.
Exprimer en fonction de x, l'aire de AMIJ, puis de CKIH et enfin la somme de ces aires.
b)Expliquer pourquoi résoudre le problème revient à résoudre l'équation 2x2 -18x+40=0
c)Développer le produit (x-5)(x-4) et conclure sur les positions de M solutions du problème.
Bonsoir
il n'est pas question de le faire
question 1 uniquement avec GeoGebra
question 2 AM =x aire du carré AMIJ
AM+MB=8 AJ+JD=10
vous pouvez en déduire l'aire du rectangle puis faire la somme des deux aires
on vous donne le résultat
développez
que vaut la moitié de l'aire du grand rectangle
Merci pour votre réponse, je dois faire cette exercice chez moi donc d'apres Vous je dois faire quoi avec geogebra ? Imprimer la figure obtenu ou autre ?
utilisez le logiciel et construire la figure
placez les points Puisque GeoGebra se sert des coordonnées
A=(0,8) B=(0,0) C=(0,10) D=(10,8)
créez un curseur M=(0,8-a) J=(a,8)
ensuite droites parallèles perpendiculaires et intersection ou vous continuez en plaçant les points avec leurs coordonnées
construction des polygones et affichage des aires
non GeoGebra est là pour s'amuser et ne sert à rien dans la résolution
aire du carré + aire du rectangle =40
le côté du carré vaut les longueurs des côtés du rectangle sont JD et MB
Donc aire carré = x*x=x2
Donc aire du rectangle =40-x2
Après je ne sais pas quoi faire enfin si c'est bon
ça c'est l'aire du rectangle
on ajoute l'aire du carré et on dit que cette somme doit être égale à 40 n'obtient-on pas ce qui est demandé ?
Aire du carré = x2 mais je ne Vois pas comment l'additionner Avec l'aire du rectangle si je fais ça je vais juste obtenir ça :
80-18x+x2+x2
80-18x+2x2
bien
Expliquer pourquoi résoudre le problème revient à résoudre l'équation
le problème est
On se propose de déterminer les propositions de M pour lesquelles la somme des aires AMIJ et CKIH est égale à la moitié de l'aire du carré rectangle ABCD
somme des aires
la moitié de l'aire du rectangle 40
égalité donc
je vais arrêter pour ce soir
D'accord vous m'avez Déjà très bien aide Merci pour votre aider, je vais essayer de me débrouiller pour la suite


