Inscription / Connexion Nouveau Sujet
Exercice Complexe
Bonjour, j'aimerais un peu d'aide.
ÉNONCÉ
Dans le plan rapporté à un repère orthormé ( O
)
On considère l'ensemble ( ) des points M d'affixe Z tels que :
) des points M d'affixe Z tels que :
1. Soit P l'application du plan dans lui même, qui a tout point M d'affixe Z associe le
point M' d'affixe Z' tel que :
on pourra poser Z = x+iy et Z' = x'+iy' ou x, y , x' et y' sont des réels.
a)Déterminer l'ensemble des points M du plan P(M) = M
b) Montrer que pour tout point M, les coordonnées du point M' vérifient x'+y'-8=0
on appelle (D) la droite décrite par les points M'.
c) Montrer que est un vecteur normal à la droite (D)
Caractériser géométriquement l'application P.
2) On se propose de déterminer l'ensemble ( ) défini au début de l'exercice.
) défini au début de l'exercice.
a) Montrer que
b) En déduire que l'ensemble ( ) est une ellipse de foyer 1+i, de directive (D), et d'excentricité 1/2.
) est une ellipse de foyer 1+i, de directive (D), et d'excentricité 1/2.
Préciser l'axe focal
j'ai déjà fait les 2 premières questions merci de m'aider pour la suite
Bonsoir,
1)c) Tu peux calculer les coordonnées du vecteur en fonction de
et
et vérifier que
où
est un vecteur directeur de
La caractérisation géométrique de (comme projection) est immédiate.
2)a) Du calcul mais je crois que tu as soit une erreur de signe soit oublié des modules.
2)b) Pense à la caractérisation d'une ellipse par foyer/directrice.
Là il va falloir que tu trouves seul:
un vecteur directeur de la droite d'équation
ce n'est pas difficile...
on appelle (D) la droite décrite par les points M'.
Ah oui c'est vrai merci beaucoup
et désolé j'ai plutôt donné un vecteur normal je crois, un vecteur directeur est ( -1 ; 1 )
Merci et bonne nuit !
on a :
Oui, mais avant de continuer, j'aimerais bien que tu me donnes ta conclusion pour 1)c) à savoir:
Caractériser géométriquement l'application P.
Oui.
Et donc à partir de:
on a :
si tu appelles
Ce la doit te rappeler un passage de ton cours sur les coniques.

Mais c'est la perpendiculaire à passant par

Bon, un dessin en cadeau (avec des informations que l'on ne te demande pas); tu pourras en faire bon usage pour déterminer les éléments de l'ellipse.
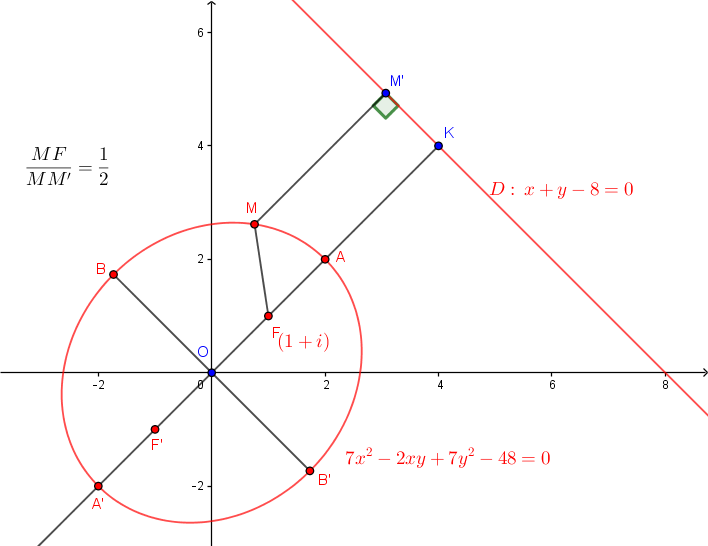

Juste un petit complément pour pfff s'il repasse par ici:
Sur le dessin figure une équation cartésienne de l'ellipse : qui n'était pas demandée et qui n'est pas du tout dans l'esprit de l'exercice. Cependant, il est utile de connaître la démarche pour l'obtenir:
Avec des équivalences entre chaque ligne:
On développe les deux membres, on réduit (calculs un peu pénibles) pour obtenir:



