Inscription / Connexion Nouveau Sujet
exercice de maths trigonométrie
Bonjour à tous,
J'aurais besoin d'aide sur un exercice de maths :
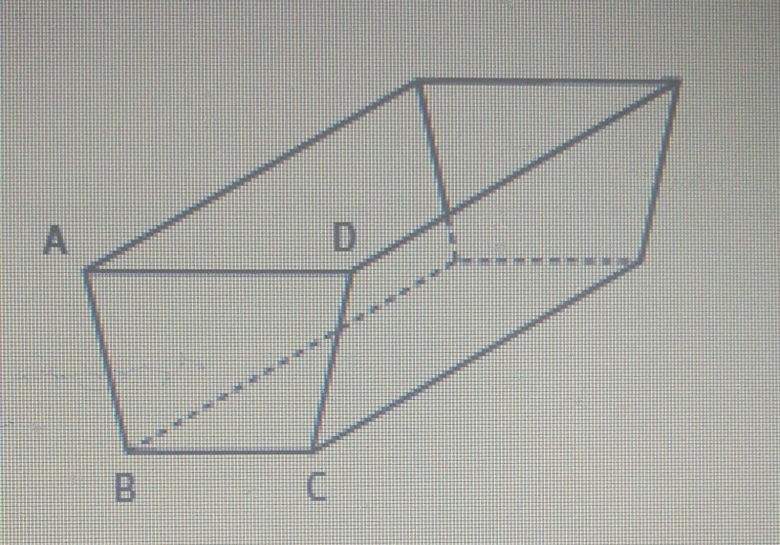
Un artisan se voit confier la construction d'un abreuvoir de forme
simple. Il opte pour un prisme droit à base trapézoïdale représenté
ci-contre en le choisissant tel que AB = BC = CD et tel que les angles
ABC et DCB aient même mesure  où
où  est un réel de [
est un réel de [ /2 ;
/2 ;  ]
]
On prendra la longueur AB comme unité de longueur.
On cherche à déterminer les valeurs de  maximisant la capacité de
maximisant la capacité de
l'abreuvoir.
1. Démontrer que l'aire f ( ) du trapèze ABCD s'écrit f(
) du trapèze ABCD s'écrit f( )=(1-cos
)=(1-cos )sin
)sin où
où 
 [
[ /2 ;
/2 ;  ]
]
2. Déterminer les valeurs de  pour lesquels le trapèze ABCD a une aire maximale puis conclure.
pour lesquels le trapèze ABCD a une aire maximale puis conclure.
De mon coté :
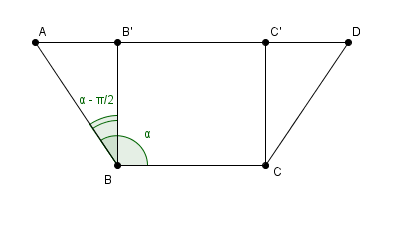
sin = opposé/hypothénuse donc sin ( -
-  /2) = AB'/AB et comme AB = 1, c'est égal à AB'
/2) = AB'/AB et comme AB = 1, c'est égal à AB'
cos = coté adjacent/hypothénuse donc cos ( -
-  /2) = BB'/AB et comme AB = 1, c'est égal à BB'
/2) = BB'/AB et comme AB = 1, c'est égal à BB'
J'ai beaucoup du mal avec la trigonométrie donc ce serait super gentil de m'aider avec cet exercice. Je ne comprends pas de quelle manière on peut trouver l'aire du trapèze et je n'ai aucune piste pour la question 2.
Merci d'avance
Bonjour,
pas de point B' sur ton schéma !!
tes explications sont donc incompréhensibles.
en devinant (on ne doit jamais deviner en lisant des explications !!)
on pourrait imaginer que BB' serait la hauteur du trapèze
et un point C' du même genre
avec AD = AB' + B'C' + C'D = 2AB' + BC
et tu connais une formule qui donne l'aire d'un trapèze non ?
(à partir de ses bases et de sa hauteur)
tu n'as qu'à remplacer les bases et hauteurs par leurs expressions en α
Bonsoir,
Merci de votre réponse.
Oui en effet, je m'excuse de ne pas avoir mis sur mon schéma les points que je nomme B' et C' mais c'est ceux que vous avez deviné.
La formule que je connais est :
(grande base + petite base) x hauteur / 2
Mais c'est la le problème... je ne comprends pas comment avoir les bases et hauteurs en  .
.
Je sais que l'angle ABC est égal à  mais j'arrive pas à déterminer les longueurs.
mais j'arrive pas à déterminer les longueurs.
Je connais sohcahtoa.
Je pense que pour connaitre la grande base, il faut donc calculer le coté adjacent mais je ne sais pas comment exploiter ces informations..
Merci de votre aide 
mais tu l'as dit !!!
cos (
 -
-  /2) = BB'/AB et comme AB = 1, c'est égal à BB'
/2) = BB'/AB et comme AB = 1, c'est égal à BB'la hauteur du trapèze est donc cos (α - π/2)
et pareil pour AB' avec le sinus
d'où on tire AD comme j'ai dit
avec AD = AB' + B'C' + C'D = 2AB' + BC
après pour réduire tout ça et obtenir la formule de l'énoncé il faudra utiliser les
angles associés
voir cours, rappel (de première) :
en particulier "Résultats à savoir retrouver sur le cercle trigonométrique"
Bonjour,
Merci de m'avoir répondu si rapidement.
Oui, j'ai compris comment il faut procéder.
Maintenant que j'ai la hauteur, je souhaite calculer la grande base.
sin( -
- /2) = AB'/AB et comme AB=1, c'est égal à AB'.
/2) = AB'/AB et comme AB=1, c'est égal à AB'.
Comme vous l'avez dit :
AD = AB'+B'C'+C'D = 2AB'+BC
donc 2(sin -
- /2) + BC
/2) + BC
Mais je n'arrive pas à calculer la longueur BC
Je sais que B'BC est égal à  /2 mais je ne comprends pas comment calculer BC en ayant uniquement cette valeur sauf si je dois également utiliser l'angle
/2 mais je ne comprends pas comment calculer BC en ayant uniquement cette valeur sauf si je dois également utiliser l'angle  ..
..
Je vais lire ce que vous m'avez mis pour savoir comment réduire tous ces sinus et cosinus 
Merci d'avance
Ah oui!
Que je suis bête...
Du coup j'ai :
--> hauteur : cos( -
- /2)
/2)
--> grande base : 2sin( -
- /2) + 1
/2) + 1
--> petite base : 1
L'aire du trapèze = [2sin( -
- /2)+1] + 1 * cos(
/2)+1] + 1 * cos( -
- /2) et le tout divisé par 2.
/2) et le tout divisé par 2.
J'ai lu attentivement la fiche dont vous m'avez mis le lien mais aucune formule ne contient : x -  /2
/2
Il y a uniquement :  /2 - x ce qui nous aide pas dans la formule que je dois simplifier.
/2 - x ce qui nous aide pas dans la formule que je dois simplifier.
Ou peut-etre suis-je passé à coté d'une information précise?
L'aire du trapèze = ([2sin(α-π/2)+1] + 1) * cos(α-π/2) et le tout divisé par 2.
parenthèses rouges obligatoires
parenthèses vertes inutiles
"le tout" inutile car divisé par 2 veut dire que c'est le tout qui est divisé par 2 :
a*b/c = (a*b)/c car les opérations de multiplication et de division ayant la même priorité sont effectuées de gauche à droite.
de même un b/2a doit être compris en toute rigueur comme (b/2)*a (même priorité donc de gauche à droite
b/2a est totalement identique à b/2*a il n'y a pas de "multiplication implicite" plus prioritaire qu'une multiplication explicite, c'est exactement pareil les deux.
et pour dire en toute rigueur on doit écrire b/(2a) parenthèses obligatoires
tout ça à cause de la priorité des opérations vues en 5ème.
(2sin(α-π/2) + 1 + 1)*cos(α-π/2)/2 veut très précisément dire
on calcule α - π/2
on en prend le sinus
on le multiple par 2
on ajoute 1
puis à ce résultat on ajoute encore 1 (deux additions de suite (a+b)+c = a+b+c)
puis ce résultat tout entier (à cause des parenthèses rouges) on le multiple par cos(α - π/2)
et ce dernier résultat (=le tout) on le divise par 2
par contre ce que tu avais écrit est faux. (outre la faute de frappe sur π/2)
[2sin(α-π/2)+1] + 1 * cos(α-π/2) et le tout divisé par2
veut dire :
on calcule α - π/2
on en prend le sinus
on le multiple par 2
on ajoute 1
puis séparément car la multiplication est plus prioritaire que l'addition
on calcule 1 * cos(α-π/2)
et c'est ce résultat là qu'on ajoute à [2sin(α-π/2)+1]
a+b*c veut dite a+(b*c) quels que soient les espaces qu'on pourrait mettre ou pas là dedans.
après ce rappel sur la façon correcte d'écrire des formules (que ce soit ici ou dans un logiciel c'est pareil : priorité des opérations et toujours et encore)
x-π/2 = -(π/2 - x) et on applique successivement deux formules :
celle de -x et celle de π/2 - x
Merci pour toutes ce explications sur les parenthèses, c'est plus clair.
Mais je n'arrive toujours pas à simplifier mon numérateur pour tomber sur ce que l'on me demande dans mon énoncé. J'ai appliqué le fait que x -  /2 = - (
/2 = - ( /2-x)
/2-x)
J'obtiens ce numérateur : voir photo
"on applique successivement deux formules : celle de -x et celle de π/2 - x"
Je ne comprends pas ce que vous voulez dire par ça...
Merci d'avance
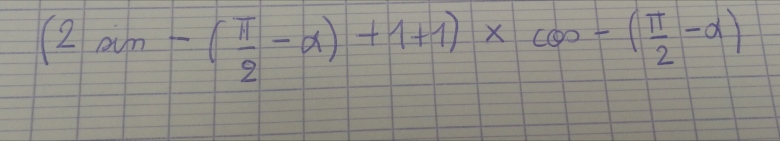
sin(α-π/2) = sin(-(π/2-α)) (on n'a rien changé du tout, c'est juste une façon différente de l'écrire)
= -sin(π/2-α) en vertu de la forme sin(-x) = -sin(x)
= - ... en vertu de la formule sin(π/2-x) = ...
-sin( /2-
/2- ) en vertu de la formule sin(
) en vertu de la formule sin( /2-x) = -cos x donc - cos(
/2-x) = -cos x donc - cos( )
)
cos( -
- /2) = -cos(
/2) = -cos( /2-
/2- = - sin(x)
= - sin(x)
Est-ce correct?
merci
sin(α-π/2) = -cos(α) est correct
par contre pour le cosinus c'est faux
cos(-x) = +cos(x) !!
donc cos(α-π/2) = +cos(π/2-α)
D'accord.
Donc il y avait juste mon signe de faux?
Car si cos(α-π/2) = +cos(π/2-α) alors c'est aussi égale à sin( ) non?
) non?
tout à fait.
et il suffit d'appliquer tout ça à la formule
aire = (2sin(α-π/2) + 1 + 1)*cos(α-π/2)/2
et de simplifier pour terminer cette question là.
(qui au passage en Terminale n'aurait pas dû prendre autant de temps,
après ces préliminaires la vraie question est la question 2 : maximum d'une fonction avec des sinus et cosinus dedans, calcul de dérivée etc)
Merci pour toute votre aide sur cette première question.
Pourriez-vous me donner une piste pour la seconde s'il vous plait?
calculer la dérivée pour trouver le maximum (déja dit)
dérivée d'un produit uv, chacun des u et v étant avec des sinus ou cosinus dedans.
Les fonctions sinus et cosinus sont dérivables sur R.
dérivée de cos (x) = -sin (x)
donc dérivée de - cos (x) = sin (x)
dérivée de sin (x) = cos (x)
Est-ce juste?
oui et donc ça fait quoi dans la fonction aire(α) = (1-cos(α))*sin(α)
(dérivée d'un produit etc)
que la variable s'appelle α ou x ou t ou etc ne change rien du tout, ce n'est que de l'écriture.
et il faudra bien faire attention à faire une étude en fonction de α et pas d'un "x" qui n'existe nulle part ici (rédaction !)
et attention que ici la fonction aire(α) n'est définie (énoncé !!) que sur [π/2; π]
on n'a donc même pas besoin d'étudier sur R entier ni même sur une période complète.
certainement pas !
comment calcules tu la dérivée d'un produit u*v ?
u ici c'est 1-cos(α)
et v c'est sin(α)
u = 1 - cos( )
)
u' = 1 - sin( )
)
v = sin( )
)
v' = cos( )
)
(u*v)'(x) = 1 - cos( ) * cos(
) * cos( ) * 1 - sin(
) * 1 - sin( ) * sin(
) * sin( )
)
Et maintenant?
u' est faux (doublement faux)
et ta formule finale est illisible (ce qu'on en lit est archi faux, priorité des opérations et parenthèses, encore et encore et toujours...)
et déja au fait c'est quoi la dérivée de u*v (avec des u, u,' v, v' ??
je dois quitter mais tu trouveras bien quelqu'un pour prendre la relève en attendant demain ou ce soir très tard.
La formule que j'ai voulu utiliser est :
(u*v)'(x) = u(x) * v'(x) + u'(x) * v(x)
Je ne sais pas si vous parliez de cette faute là ou même si j'ai utilisé la bonne formule mais j'avais mis un * à la place d'un +
u' est faux par rapport au signe du sin ou par rapport à quelque chose d'autre?
D'accord, à bientot!
pour u' : deux fautes
le signe
et le fait que la dérivée de la constante 1 est 0, pas 1.
la formule en u et v est bonne mais pour son application :
il fallait deviner le + tout de même !!
et de toute façon il manque des parenthèses :
1 - cos(α) * cos(α) veut dire (priorité encore et encore disais-je)
on commence par multiplier cos(α) * cos(α) car la multiplication est prioritaire par rapport à l'addition / soustraction
puis on retranche ce produit de 1
ce qui est faux
alors que avec u = 1 - cos(α) et v' = cos(α)
u*v' = (1 - cos(α))*cos(α)
parenthèses rouges absolument obligatoires.
et puis comme u' est faux ...
(mais avec ton u' faux il aurait là aussi fallu pour écrire le u'v correctement des parenthèses obligatoires que tu as complètement oubliées ! )
Bonjour,
(u*v)'(x) = [(1 - cos( )) * (cos(
)) * (cos( ))] + [(sin(
))] + [(sin( )) * (sin(
)) * (sin( ))]
))]
J'ai compris ma faute, est-ce bon maintenant?
oui,
mais tu n'as toujours pas compris ces histoires de parenthèses car là tu en mets trop (des inutiles)
(1-cos(α))*cos(α) + sin(α)*sin(α) suffit
celles là sont obligatoires
toutes les autres que tu rajouterais sont superflues et ont pour résultat de rendre l'expression bien moins lisible surtout !!
développer simplifier etc
ensuite plusieurs pistes (car ce n'est pas évident) :
tout écrire avec uniquement des cosinus car cos² + sin² = 1
on aboutit à un trinome du second degré en X = cos(α)
ou utiliser les formules de duplication (cos(2x) = ...) pour aboutir à une équation cos(u) = cos(v) que tu sais résoudre
ou utiliser des formules certainement pas vues en Terminale en particulier la transformation de cos(p)-cos(q) en produit
on obtient alors f'(α) = 2sin(3α/2)sin(α/2) qui est loin d'être évident à obtenir à ce niveau.
cette dernière façon de procéder donne toutefois non seulement les solutions de f'(α) = 0 mais quasi directement le signe de f'(α)
rappel : pour trouver minima et maxima de f, on étudie les variations de f, c'est à dire le signe de la dérivée, écrire que la dérivée est nulle ne suffit pas pour affirmer que ce serait un maximum, un tableau de variations est nécessaire
évidemment j'élimine (on est en Terminale tout de même) la solution de facilité qui consiste à regarder ça sur l'écran de sa calculette...
quitte à prouver juste par le calcul que la valeur exacte devinée (on dit conjecturée) est bien exactement vraie
Bonsoir,
Oui d'accord. Donc maintenant que j'ai la dérivée, il faut que je fasse un tableau de variations à partir de f(x) et de x non?
Mais quelles valeurs dois-je mettre dans les x?
J'ai pas vu comment faire un tableau de variations avec des valeurs de cosinus et sinus...
Merci d'avance
quelle que soit la fonction que ce soit avec des cosinus, des polynomes etc etc ou n'importe quoi, la démarche est toujours la même :
on étudie le signe de la dérivée f'(x) dans son domaine de définition
et c'est à partir de cette étude de signe qu'on trouve les valeurs à mettre dans le tableau
pas le contraire !!
donc à faire (déja dit)
étudier le signe de la dérivée (1-cos(α))*cos(α) + sin(α)*sin(α) (de cette fonction de la variable α)
et comme cette fonction est continue les changements de signes éventuels ne se produiront qu'à des valeurs de α pour lesquelles f'(α) = 0
donc première chose à faire :
résoudre (1-cos(α))*cos(α) + sin(α)*sin(α) = 0
et ça se fait comme j'ai dit
commencer par "améliorer" cette écriture
(développer, et sin(α)*sin(α) ça s'écrit sin²(α) etc et comme j'ai dit)
les valeurs à mettre dans le tableau c'est :
les valeurs de α définissant le domaine de définition : π/2 et π (énoncé)
et les valeurs de α qui annulent f'(α) (les solutions de l'équation citée juste au dessus qui sont dans ce domaine là, les autres on s'en fiche)
donc retrousser ses manches et faire ce que j'ai déja dit...
Bonjour,
Je sais ca. Mais de quelle manière cette formule m'aide-t-elle pour 1 - cos( ) * cos (
) * cos ( )?
)?
Car même si je met cos en "a", ca ne fonctionne pas à cause du 1 -
mais bon sang de bois ce n'est pas et ce n'a jamais été
1 - cos( ) * cos (
) * cos ( )
)
c'est (1 - cos( ) )* cos (
) )* cos ( )
)
ça vient dès le départ de la formule de l'aire du trapèze qui n'est pas a+b*h/2 = mais (a+b)*h/2 =
ta façon d'écrire fausse dès le départ et ton incompréhension profonde des opérations qui sont réellement effectuées en est plus que responsable
tes erreurs sont tellement ancrées en toi que au bout de deux lignes de calcul elles reviennent en force !
tu DOIS corriger ça au plus profond de toi de TOUTE URGENCE
des erreurs à la rigueur tolérables en 3ème ne le sont plus en Terminale !!!
tu n'as toujours rien de rien compris aux bases des bases du calcul ??
c'est niveau collège ces calculs de développement
les morceaux qui relèvent du niveau Terminale sont très peu nombreux dans cet exo !