Inscription / Connexion Nouveau Sujet
Exercice fonction ( avec courbes)
Bonjour à tous
Je bloque vraiment sur cet exercice
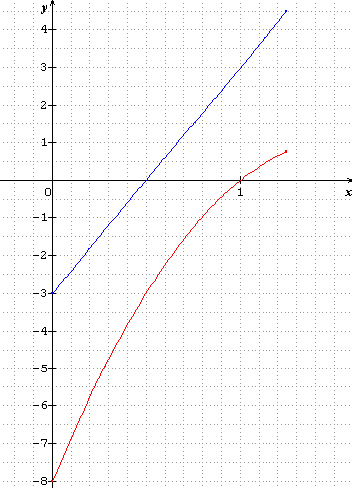
Pour x appartenant à l'intervalle [0;5/4] on a representé ci-contre les fonctions f et g définies par :
f (x) = 1-(2-3x)2 et g(x) = 6x-3
Résoudre graphiquement l'équation f(x) = g(x) et l'inéquation f(x)<g(x)
Je ne sais vraiment pas commment procéder.
Merci d'avance
NOn mais enfaite les courbes sont déja tracés!!
Mais je ne sais pas comment faire!!
C'est bien les mêmes courbes que je t'ai tracé ?
Qu'est ce que tu ne comprends pas : tracer les courbes ? résoudre l'équation ? l'inéquation ?
En faite résoudre l'équation et l'inéquation graphiquement je ne sais pas comment faire
Bisous et je te remercie déja
On dit de resoudre sthg graphiquement , c'est a dire en n'utilisant que le graphique ( logique ) il suffit donc de voir les courbes et leur "position" l'une par rapport a l'autre dans ce cas.
Pour prouver que f(x)=g(x)
il suffit de voir, a partir de la courbe toujours, a quel abscisse les deux courbes se "croisent".
Dans ton cas , si tu ne t'es pas trompé : l'ensemble des solutions est S=
Pour prouver que f(x) < g(x) , il suffit de voir dans quel intervalles , la representation graphique de la fonction g est " au dessus " de la fonction f ici
L'ensemble des solutions est S=[0;5/4]
J'ai été le plus clair possible ? As-tu des doutes sur autres choses?