Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Exercice nombre complexe

Posté par
Synyster 12-12-10 à 01:31

Bonsoir à tous, j'ai un DM de maths à faire, qui a une difficulté de 3 étoiles, ce qui est le plus haut niveau alors que j'ai un niveau en maths moyen et je ne comprend vraiment pas les nombres complewes donc je n'arrive pas à le faire. Votre aide serait la bienvenu.


Le plan complexe P est rapporté au repère orthonormal direct (O,u,v) avec 2cm comme unité graphique.
On note f l'application du plan P privé de O dans P qui, à tout point M d'affixe z non nule, associe le point M' d'affixe z'= 1/conjugué de z.

On a donc aussi z'=z/(module de z)²

1) Montrez que O, M t M' sont align"s

2) Déterminez l'ensemble R des points invariants par f. Vérifiez que R contient les points A et B d'affixes respectives -1 et i.

3) Soit C le cercle de diamètre [A B], E le milieu de [A B]et E'=f(E)
Déterminez une équation cartésienne de C.
Montrez que E' appartient à C.

4) Le point M d'affixe z étant un point quelconque de la droite (AB), on se propose de construire son image M' d'affixe z' par l'application f.

a) Déterminez une équation cartésienne de la droite (AB)
On pose k=OM², z=x+iy et z'=x'+iy', avec x,y,x' et y' réels.
Exprimez en fonction de x.
Montrez que M' appartient à C ( Vous pourrez exprimer x' et y' en fonction de x et k )

b) Déduisez des questions précédentes une construction géométrique du point M' connaissant le point M

Posté par
dhaltere : Exercice nombre complexe 12-12-10 à 09:35

Euh, et tu n'as répondu à aucune des questions, même pas la première, qui est loin d'être "3 étoiles" ?

Posté par
Synysterre : Exercice nombre complexe 13-12-10 à 21:06

J'essaie de le faire mais je n'y arrive vraiment pas si on pouvait me mettre au moin sur la piste

Posté par
dhaltere : Exercice nombre complexe 13-12-10 à 21:45

5$z'=\frac1{\bar z}=\frac1{z\bar z}z=\frac1{|z|^2}z

Puisque 5$\frac1{|z|^2} est un réel, alors z' est proportionnel à z : 0, z et z' sont les affixes de points alignés.

Posté par
Synysterre : Exercice nombre complexe 15-12-10 à 15:31

Merci de ton aide mais bon je comprend toujours pas comment montrer que les points sont alignés

Posté par
dhaltere : Exercice nombre complexe 15-12-10 à 16:18

Je crois que tu manques un peu d'imagination.

Le nombre complexe 5$0=0+i0 est associé au point O du plan de coordonnées 5$(0;0)
5$z=x+iy est associé à un point M du plan de coordonnées 5$(x;y)
5$z'=\frac{1}{|z|^2}z=\frac1{x^2+y^2}(x+iy) est associé au point M' du plan de coordonnées 5$(\frac{x}{x^2+y^2};\frac{y}{x^2+y^2})

Reste à prouver avec les techniques habituelles (mais les maitrises-tu ?) que les point O, M et M' sont alignés.

Posté par
Synysterre : Exercice nombre complexe 15-12-10 à 17:02

Il faut ensuite que je calcul les coordonnées des vecteurs OM et MM' et que je prouve que OM = k MM'  ?
Et pour le 2) je trouve :

Un point M d'affixe z est invariant par f si, et seulement si, sont image M' a pour affixe z .
D'où M d'affixe z est invariant par f si, et seulement si, z = 1/conjugué de z ou z * conjugué de z = 1 .
Or  z * conjugué de z  représente le module de z au carré (avec z = x + iy , z  = (x + iy)(x - iy) = a² + b² )
Donc M d'affixe z est invariant par f si, et seulement si, (module de z)²  = 1 ou module de z = 1 .
Conclusion : L'ensemble des points invariants par f est le cercle de centre O et de rayon 1 .

Est ce juste ? Merci de ton aide

Posté par
dhaltere : Exercice nombre complexe 15-12-10 à 17:12

5$\vec{OM^'}=\frac1{x^2+y^2}\vec{OM} donc ils sont alignés. Les félicitations du Jury.

Posté par
Synysterre : Exercice nombre complexe 15-12-10 à 22:31

Merci beaucoup
Pour le 3) j'ai fais:
L'équation cartésienne d'un cercle est égal à son rayon au carré.
Calculons la longueur AB
Je trouve AB= racine de 2 donc l'équation cartésienne = 1/2

Est ce juste ?
Et pour montrer que E' appartient à C j'ai calculé les coordonnées de E, est ce utile ou est ce que je ne suis pas sur la bonne voie ?

Posté par
dhaltere : Exercice nombre complexe 16-12-10 à 11:03

Citation :
Pour le 3) j'ai fais:
L'équation cartésienne d'un cercle est égal à son rayon au carré.

faux

Posté par
Synysterre : Exercice nombre complexe 16-12-10 à 12:07

En cherchant sur internet c'est la formule que j'ai trouvé, peux tu me la donné si celle ci est fausse ? Et est ce que je suis sur la bonne voie pour la suite ?

Posté par
dhaltere : Exercice nombre complexe 16-12-10 à 13:06

Citation :
L'équation cartésienne d'un cercle est égal à son rayon au carré


ce n'est pas une formule; tout juste un pense-bête. et incomplet.
Qu'est-ce que tu espères faire avec un truc pareil ?

Posté par
Synysterre : Exercice nombre complexe 28-12-10 à 15:18

C'est ce que je trouve sur internet ou alors je le comprend mal, pourrais tu m'expliquer comment faire alors ?

Posté par
dhaltere : Exercice nombre complexe 28-12-10 à 17:25

Tu ferais mieux d'apprendre un peu ton cours et de ne pas croire béatement qu'Internet saura toujours t'apporter tes solutions sans effort.
Mais c'est Noël, alors cadeau :

On note f l'application du plan P privé de O dans P qui, à tout point M d'affixe z non nulle, associe le point M' d'affixe 5$z'=\frac{\,1\,}{\bar z}

On a donc aussi 5$z'=\frac{z}{\bar zz}=\frac{z}{|z|^2}

1) Montrez que O, M et M' sont alignés
5$|z[^2 est réel, donc z' et z sont proportionnels, donc O, M et M' sont alignés
5$\vec{OM'}=\frac{1}{|z|^2}\vec{OM}=\frac{1}{OM^2}\vec{OM}

2) Déterminez l'ensemble R des points invariants par f. Vérifiez que R contient les points A et B d'affixes respectives -1 et i.
Trouver les points invariants, c'est résoudre l'équation 5$z'=z

donc
5$z\bar z=1
donc
5$|z|^2=1
donc
5$|z|=1

Cette dernière équation caractérise les points du cercle unité, cercle centré sur l'origine du repère, de rayon 1.
Il est alors clair que 1, -1, i et -i font partie des points invariants.


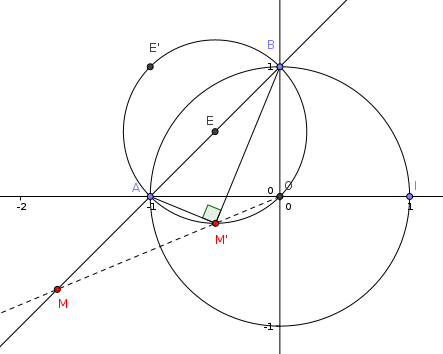
3) Soit C le cercle de diamètre [A B], E le milieu de [A B]et E'=f(E)
Déterminez une équation cartésienne de C.
A d'affixe -1
B d'affixe i
Leur milieu E a pour affixe 5$z_E=\frac{-1+i}2
le cercle a pour équation
5$(x+\frac12)^2+(y-\frac12)^2=r^2
et pour déterminer r^2, il suffit d'écrire que A appartient au cercle
5$(-1+\frac12)^2+(0-\frac12)^2=r^2 \\ \frac14+\frac14=r^2 \\ \frac12=r^2

Le cercle a donc pour équation
5$(x+\frac12)^2+(y-\frac12)^2=\frac12
Son rayon est 5$\frac1{\sqr2}=\frac{\sqr2}2 et il passe par l'origine.

Montrez que E' appartient à C.

Calcul de l'image 5$z_{E'} de 5$z_E
5$z_{E'}=\frac{1}{\frac{-1-i}2}=\frac2{-1-i}=\frac{2(-1+i)}{1^2+1^2}=-1+i

E' a pour coordonnées (-1,1), et on vérifie aisément que celles-ci vérifient l'équation du cercle C.

4) Le point M d'affixe z étant un point quelconque de la droite (AB), on se propose de construire son image M' d'affixe z' par l'application f.

a) Déterminez une équation cartésienne de la droite (AB)
5$y=x+1
Montrez que M' appartient à C

M sur (AB) donc 5$z=a+m(b-a), avec m réel quelconque.
On va procéder autrement : on va montrer que (M'A) et (M'B) sont perpendiculaires

Pour cela, il suffit de montrer que 5$\bar{(z'-a)}(z'-b) est un imaginaire pur

5$a=-1 \\ b=i \\ z=a+m(b-a)=m-1+im \\ \bar z=m-1-im \\ z\bar z\in\mathbb{R}
5$\bar{(z'-a)}(z'-b)=(\frac1z+1)(\frac{\,1\,}{\bar z}-i)=\frac{1}{z\bar z}+\frac{\,1\,}{\bar z}-\frac{\,i\,}{z}-i=\frac{1+z-i\bar z}{z\bar z}-i= \\ \frac{1+m-1+im-i(m-1-im)}{z\bar z}-i=-i

b) Déduisez des questions précédentes une construction géométrique du point M' connaissant le point M

Tracer la demi-droite [OM). M' est à l'intersection avec le cercle C

Exercice nombre complexe

Posté par
Synysterre : Exercice nombre complexe 02-01-11 à 02:29

Je te remercie grandement, j'ai fait les explications là ou il y en avait peu comme par exemple la détermination de l'équation cartésienne de la droite (AB). Par contre " exprimer k en fonction de x " me pose un problème


Rechercher
Menu
Espace membre
6 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1741 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !