Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Angles orientésTopics traitant de angles orientés [tout]Lister tous les topics de mathématiques

1 2 3 +

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 21:03

3$\rm Voila^, le point M et l^,angle x

exercice sur les angles orientés

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 21:06

Ah merci. C'était là que je pensais.

Il faut ensuite calculer sin x, c'est encore avec les produits scalaires ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 21:15

3$\rm coc x=-\frac{1}{2} donne 2 valeurs de x comme tu vois sur le cercle trigonome$,trique

3$\rm soit x=\frac{2\pi}{3} soit x=\frac{4\pi}{3}

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 21:18

Oui mais il faut calculer sin x, c'est pas soit 3/2 soit -3/2 ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 21:32

3$\rm La question 2 est plus subtile on te demande pas de calculer sinx\\on te donne un intervalle de x\in[5\pi ; \frac{11\pi}{2}]\\a^, toi de trouver x dans cet intervalle comprends-tu cela?\\je te propose de bien relire la question et de me repondre

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 21:36

Oui, j'ai relu la question.

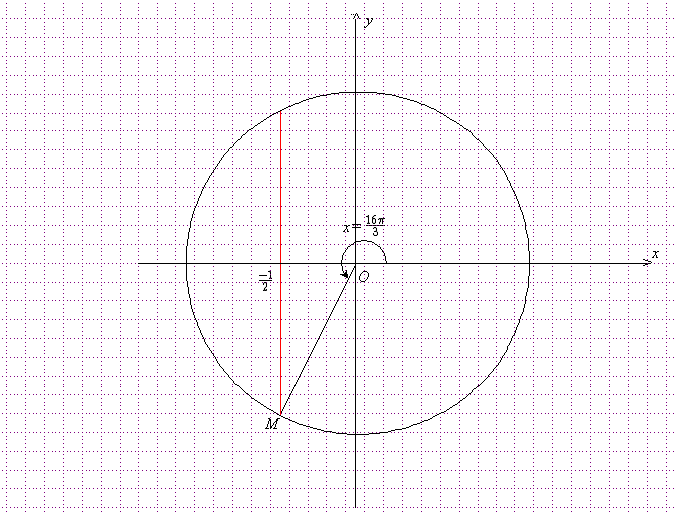
Mais la question 3)a) demande de placer le point M et de calculer sin x pourtant.
Et la question 3)b) demande de trouver x.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 21:44

3$\rm Oui mais avant on te donne un intervalle et un cosx=-\frac{1}{2} il faut placer\\le point M sur le cercle (Soit en haut soit en bas) tout depend de l^,intervalle\\ donne^, une fois tu as plcer le point M sur le cercle sinx est imme^,diat\\le plus difficile c^,est d^,e^,crire toutes les solutions de cosx=-\frac{1}{2}\\sais-tu le faire?

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 21:47

Je suis désolée mais non je ne sais pas faire.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 21:58

3$\rm cosx=-\frac{1}{2} \Longrightarrow cosx=\pm cos(\frac{2\pi}{3})+2 \mathbb{K}\pi \\avec \mathbb{K} \in \mathbb{Z}

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:01

3$\rm il faut maintenant chercher la valeur de \mathbb{K} pour que x tombe dans\\ l^,intervalle impose^, dans l^,enonce^, a^, savoir x\in [5\pi ; \frac{11\pi}{2}]

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:02

Oui d'accord, donc ça c'est toutes les solutions de cos x = -1/2 ?

Mais ça répond à quelle question ? Je comprend pas.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:06

3$\rm on repond a^, la question 3) a) on cherche x puis on enchaine pour chercher sinx

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:07

3$\rm pas facile cette question, je trouve, pour une classe de premie^,re! j^,avoue

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:09

Oula, et comment fait-on pour trouver K ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:12

3$\rm \mathbb{K} \in \mathbb{Z}\\\mathbb{K}=1,2,3,4,5,...etc...

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:13

3$\rm j^,ai oublie^, le ze^,ro\\\mathbb{K}=0,1,2,3,4, ... etc...

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:15

Donc K peut être n'importe quoi dans Z ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:16

3$\rm tout a^, fait

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:17

3$\rm on revient au proble^,me il te faut une valeur de \mathbb{K}\\tel que x soit dans l^,intervalle

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:18

D'accord.

Mais que doit-on faire après ? On a pas répondu à la question là si ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:19

3$\rm non pas encore il faut chercher x dans l^,intervalle

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:21

Mais comment fait-on ça ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:22

3$\rm attends je construit mon message

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:35

3$\rm Nous avons :\\cos x=-\frac{1}{2} on a vu que ceci nous donne:\\ x=\pm\frac{2\pi}{3})+2\mathbb{K}\pi\\je prends x=+\frac{2\pi}{3}+2\mathbb{K}\pi\\k=1 donc x=\frac{2\pi}{3})+2\pi=\frac{8\pi}{3}\\ne convient pas car nous sommes pas dans l^,intervallepour k=2 on sort de l^,intervalle\\k=3 on sort de l^,intervalle\\que faire?\\on prend les valeurs ne^,gatives (n^,oublie pas le \pm )\\x=-\frac{2\pi}{3}+2\mathbb{K}\pi\\pour k=1\\-\frac{2\pi}{3}+2\pi=\frac{4\pi}{3} (hors intervalle)\\pour k=2\\-\frac{2\pi}{3}+4\pi=\frac{10\pi}{3} (hors intervalle)\\pour k=3\\-\frac{2\pi}{3}+6\pi=\frac{16\pi}{3} OUF celui-ci convient puisque \frac{16\pi}{3}=\frac{32\pi}{6} juste avant \frac{11\pi}{3}\\puisque \frac{11\pi}{3}=\frac{33\pi}{6}\\et \frac{32\pi}{6}<\frac{33\pi}{6}

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:38

3$\rm sur mon cercle trigonome^,trique j^,ai mis x=\frac{16\pi}{3}\\maintenant tu comprends pourquoi

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:39

D'accord ok.

Ce qui veut dire que K = 6 ?

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:41

Non mince K = 3 pardon.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:42

3$\rm non k=3 tu as vu 6 a^, quelle ligne ?\\de toute facon on oublie k maintenanr nous avons notre angle\\c^,est l^,essentiel tu ne crois pas?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:44

3$\rm de^,sormais calculer sinx est un jeu d^,enfant\\puisque x=\frac{16\pi}{3}\\il faut donc calculer sin(\frac{16\pi}{3})\\je te laisse faire vas-y

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:45

Oui, donc l'angle x = 16/3 ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:46

3$\rm Oui x=\frac{16\pi}{3} comment tu calculerais sin(\frac{16\pi}{3})?pour repondre a^, la question 3) a)

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:48

Faut y taper à la calculatrice non ?

On ne peut pas y lire sur le cercle.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:50

3$\rm Non on calcul pas comme cela\\On de^,compose \frac{16\pi}{3} en multiple de 2\pi\\ici \frac{16\pi}{3}=6\pi-\frac{2\pi}{3}\\donc calculer sin(\frac{16\pi}{3})\\revient a^, calculer sin(6\pi-\frac{2\pi}{3})=sin(-\frac{2\pi}{3})=-sin(\frac{2\pi}{3})=-\frac{\sqrt{3}}{2}

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:53

Ohlala, mais je n'ai jamais fait ça !!
Merci j'ai compris.

Donc sin x = -3/2.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:54

3$\rm Je te propose de relire la question 3) a) on a donc repondu a^, la question 3) a)\\tu es d^,accord?

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 22:55

Oui, je suis d'accord. On connaît sin x maintenant.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 22:58

3$\rm On connait sinx et x\\a^, la dernie^,re question on te demande de montrer que :\\(OM)\perp(AB)

3$\rm tu as une ide^,e ?

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 23:02

Il faut faire le produit scalaire de OM et AB ?

Non je sais pas, je vois pas. Désolée.

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 23:03

3$\rm Tre^,s bien le produit scalaire c^,est la bonne reponse

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 23:04

Ah bon, j'ai juste ?!

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 23:06

3$\rm Oui c^,est juste mais comment tu vas faire ce produit scalaire?

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 23:08

Il faut d'abord calculer les coordonnées de OM.
Ensuite, calculer la norme de OM car AB on a déjà.
Et appliquer la formule.
Non ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 23:10

3$\rm tu n^,as pas besoin de normer ton vecteur pour calculer le produit scalaire

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 23:11

Ah, alors il faut utiliser cette formule : AB.OM = x x' + y y' ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 23:12

3$\rm En fait, 2 vecteurs perpendiculaire si et seulement si leur produit scalaire est nul

3$\rm Donc il faut traduire ceci :\\\vec{OM}.\vec{AB}=0

3$\rm Ecris \vec{OM} dans le repe^,re (O, \vec{i}, \vec{j}) puis e^,cris \vec{AB} dans ce meme repe^,re

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 23:15

Euh pardon mais ça veut dire quoi d'écrire OM et AB dans un repère ?

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 23:17

3$\rm j^,attendais cette question

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 23:20

3$\rm souviens-toi pour e^,crire le vecteur \vec{AB}\\on avait e^,crit \vec{AB}=\vec{OB}-\vec{OA}=-\frac{3}{2}\vec{i}+\frac{\sqrt{3}}{2}\vec{j} c^,est cela e^,crire un vecteur dans une base

Posté par
camillemre : exercice sur les angles orientés 19-04-10 à 23:23

3$\rm \vec{OM}=cosx\vec{i}+sinx\vec{j}=-\frac{1}{2}\vec{i}-\frac{\sqrt{3}}{2}\vec{j}

3$\rm \vec{AB} (de^,ja^, calcule^,)

3$\rm il ne te reste plus qu^,a^, calculer \vec{OM}.\vec{AB} et voir si ce produit donne ze^,ro\\si c^,est le cas alors \vec{OM}\perp\vec{AB}

Posté par
miss-rockre : exercice sur les angles orientés 19-04-10 à 23:24

Ah d'accord, il faut utiliser les coordonnées du vecteur en question.

Les coordonnées de OM sont (-1/2;-3/2).

Donc pour OM = OM - OO = -1/2 - 3/2 ?

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !