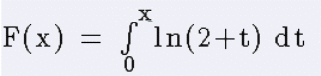Bonjour

En notant f une primitive de
On a :

On a ainsi :
(car f(0) est une constante donc sa dérivée est nulle)
c'est à dire :


c) étudies alors le signe de cette dérivée


Jord

Bonjour,
La ya un truc qu'il faut m'expliquer, j'ai du mal comprendre un truc sur les intégrales.

Vu que ya un "0" avant l'intégrale, F(x), ne serait pas nulle pour tout t de l'ensemble de défintion???
Par conséquent, la dérivée de cette fonction est nulle aussi, non??
Me trompe-je???


Ayoub.

>Schumi

Oui tu te trompes car ce n'est pas écrit correctement :

le zéro est la borne basse de l'intégrale
le x en est la borne haute

Vive le LaTeX !

Philoux

bien vu philoux

>> 1 Schumi 1 :

tu aurais préféré le voir écrit comme ça ?  :



@+ sur l'

>Salut Lyonnais

Et pourquoi pas le x à droite du signe somme ?



Philoux

Re

parce que sino on aurait un truc du style :



ce qui ne veut absolument rien dire ...

@+

Et pourquoi pas :



Jord

>romain

On ne sait pas écrire celà, en LaTeX ?

Philoux

Ah ben comme ca je comprends mieux, parce que je me disais que cété un peu idiot de donner a des élèves une fonction nulle??!!
Enfin, bo, tout est rentré ds les normes.

Ah, et au fait, koko, t'as trouvé le résultat???


Ayoub