Inscription / Connexion Nouveau Sujet
Exercices éllipses , complexes
Bonjour/Bonsoir tout le monde
Je n'arrive pas à résoudre cet exercice sur les éllipses. Pouvez vous m'aider s'il vous plaît ? Merci
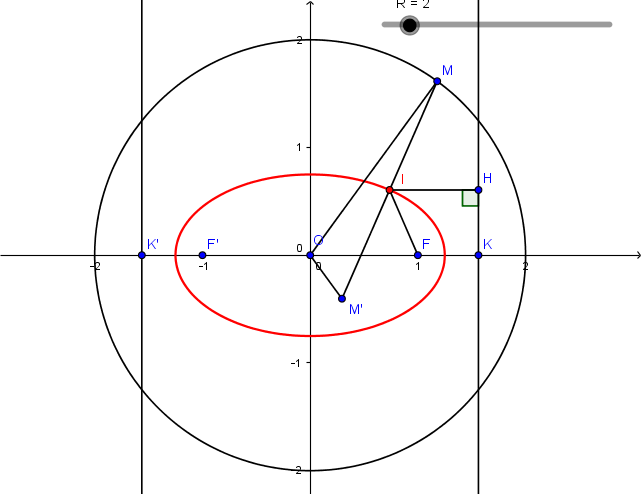
Soit C un cercle de centre O et de rayon R > 1 . A tout point M d'affixe z = Rei T du cercle C , on associe le point M d'affixe 1/z .
T du cercle C , on associe le point M d'affixe 1/z .
1. Déterminer la partie réelle et la partie imaginaire du milieu de I de [MM']
2. Montrer que I varie sur une ellipse E lorsque M varie sur C .
3. Donner les éléments caractéristiques de E.
1. z' = 1/Rei
zI = (z+z')/2
zI = (1+R²ei2 )/ 2 Rei
)/ 2 Rei
A partir de là je suis bloqué , je ne sais pas comment trouver la partie réelle et partie imaginaire de zI
Merci d'avance pour votre aide
Merci
Si je ne fais pas d'erreurs , on trouve
zI = (1+R²)cos / 2R + (R²-1)sin
/ 2R + (R²-1)sin i / 2R
i / 2R
Et on a donc la partie réelle et la partie imaginaire
2) Lorsque M varie sur C on a : xM = R cos et yM = R sin
et yM = R sin
xI = (1+R²)cos / 2R
/ 2R  cos
cos = 2R xI / (1+R²)
= 2R xI / (1+R²)
yI = (R²-1)sin / 2R
/ 2R  sin
sin = 2R yI / (R²-1)
= 2R yI / (R²-1)
On a donc x²I / ((1+R²)/4R²) + y²I / ((R²-1)/4R²) = 1
I varie sur une ellipse E
3) E est une ellipse de
_ centre O(0;0)
- de sommets A ( (R²+1/2R) ; 0) , A' ((-1-R²/2R) ; 0) , B (0 ; (R²-1/2R) ) et B' (0 ; (1-R²/2R))
_ de directrice x =[ R²+1/2R]²
_ d'excentricité e = 2R/R²+1