Inscription / Connexion Nouveau Sujet
exo nombre complexe terminale S
Bonjour, j'ai un exercice a faire sur les nombres complexes, quelqu'un pourrait-il m'aider svp ?
1) Résoudre dans C l'équation :
(iz + 1 + i 3) (z² - 2z + 4) = 0
3) (z² - 2z + 4) = 0
et donner les solutions sous la forme algébrique.
2) On considère les nombres complexes a = 1 + i 3 et b = -
3 et b = -  3 +i on appelle A et B les points d'affixes respectives a et b.
3 +i on appelle A et B les points d'affixes respectives a et b.
a) Déterminer une forme trigonométrique de a et b.
b) Placer les points a et b ( unité : 3 cm)
c) Démontrer que le triangle OAB est rectangle isocèle où O est l'origine du repère.
d) K est le milieu du segment AB. Placer K et déterminer son affixe k.
3) On considère le complexe c = ( 1 -  3) + ( 1 +
3) + ( 1 +  3) et on appelle C le point du plan d'affixe c.
3) et on appelle C le point du plan d'affixe c.
a) Montrer que K est le milieu du segment OC, puis placer C.
b) Démontrer que le quadrilatère OACB est un carré.
Bonsoir,
un produit est nul si l'un de ses facteurs est nul.
donc tu as soit: iz + 1 +i = 0 (pas très difficile à résoudre)
soit z² - 2z + 4=0 (polynôme du second degré en z)
Merci à vous Glapion et tranquilo_22,
Alors comme on sait que un produit est nul si l'un de ses facteurs est nul, on va résoudre l
z² - 2z + 4 = 0
 = b² - 4ac = (-2)² - 4 * 1² * 4 = 4 - 16 = - 12
= b² - 4ac = (-2)² - 4 * 1² * 4 = 4 - 16 = - 12
L'équation admet 2 solutions dans  :
:
x1 = -b - i -
- / 2a = -2 - i
/ 2a = -2 - i 12 / 2
12 / 2
x2 = -2 + i  12 / 2
12 / 2

Je viens de refaire mon calcul mais je trouve 2  i
i 3 mais pas 1 devant c bizarre j'ai peut-être fait une erreur alors
3 mais pas 1 devant c bizarre j'ai peut-être fait une erreur alors
Oui c'est ce que je dis, tu ne mets pas bien les parenthèses
(- (-2) + i 12) / 2 le premier 2 aussi est divisé par 2
12) / 2 le premier 2 aussi est divisé par 2
Mais non, je voulais dire si sur le forum on pouvais tracer un graphique pour faire placer les points lol
mais merci !
c) Démontrer que le triangle OAB est rectangle isocèle en O
Démontre que OA=OB (donc que |a|=|b|) et que OA est perpendiculaire à OB (donc par exemple que b=ia)
OAB est rectangle isocèle en O. Montrons le en considérant
z = zA- zO / zB- zO
Mais le problème c'est que pour faire le calcul je suis embêté parce que je sais que
ZA= 1+i 3
3
ZB= -  3 + i
3 + i
mais pour ZO on ne s'est pas.
Comme O est l'origine, ses coordonnées sont (0;0), sachant que z = x+iy alors zO= 0+ i0 c'est égal à i ?????
zO= 0+ i0 c'est égal à i ?
ben non
étonnant, non ? l'affixe de l'origine du repère est le réel 0.
A retenir, ça pourra être utile.
Pour la question c pour démontrer que le triangle est rectangle isocèle.
Je souhaite faire le calcul suivant :
z = zA- zO / zB- zO
mais je sais pas s'il est bien écrit oui s'il y a une erreur ?? (entre les zA et tout sont-ils dans le bon ordre ?
Puis je compte chercher le module et trouver un argument pour pouvoir conclure.
il manque les parenthèses
Lis bien ce qui suit :
sur ton livre, ou ton cahier, tu vois une formule du genre de celle-ci
et tu as envie de l'écrire ainsi sur le forum
a/b+c
c'est une erreur
l'écriture
a/b+c
équivaut à
l'écriture correcte est
a/(b+c)
sur ton livre, ou ton cahier, tu vois une formule du genre de celle-ci
et tu as envie de l'écrire ainsi sur le forum
a/bc
c'est une erreur
l'écriture
a/bc
équivaut à
l'écriture correcte est
a/(bc)
sur ton livre, ou ton cahier, tu vois une formule du genre de celle-ci
et tu as envie de l'écrire ainsi sur le forum
a+b/c
c'est une erreur
l'écriture
a+b/c
équivaut à
l'écriture correcte est
(a+b)/c
sinon, utilise
Tu peux apprendre à écrire des formules mathématiques avec les expressions LaTeX (prononcer latec)
il te faut encadrer tes formules par des balises spéciales.
Pour essayer, saisit cette expression ci-dessous
[tex] \frac{ -b \pm \sqrt{ b^2 - 4ac }}{ 2a } [/tex]
Clique sur le bouton "Aperçu"
et tu verras apparaître ça :
Pour apprendre et t'entraîner :
le lien de ce forum, que tu peux aussi consulter par le bouton dans la barre de boutons orange :
![]() [lien]
[lien]
Plus complet mais en anglais : ![]()
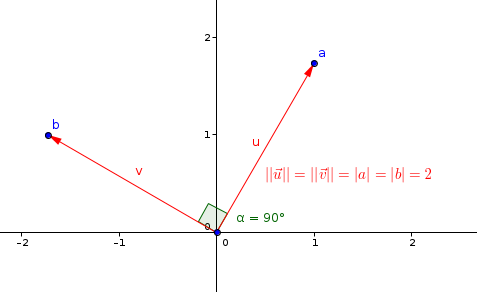
Enoncé et résultats précédents :
calcul simplicime :
donc comme disait Glapion (salut) :
et je rajoute : par conséquent |a|=|b|
interprétation géométrique : b est l'image de a par la rotation de centre O, d'angle : le triangle OAB est isocèle rectangle direct de sommet O
Merci pour l'histoire des parenthèses ! 
Mais pour les calculs je ne comprends pas les exponentielle avec puissance parce que je n'ai jamais fais cela en classe.
N'y a-t-il pas un autre moyen ? svp
si, plus lourd
on utilise le nombre conjugué car
(tu vérifieras)
il te reste à développer et simplifier
Quelqu'un pourrait m'aider svp concernant la question 2a
Comment faut-il faire pour détermnier une forme trigonométrique de a et b ?
z = r (cos  + i sin
+ i sin  )
)
z = r (cos 1/2 + i sin ( 3/2)
3/2)
??
r = module de z =  a² + b²
a² + b²
donc
module de ² =  (1+i
(1+i 3)² + ( -
3)² + ( -
 3+i)²
3+i)²
maisj pouvez me faire le calcul svp ? Je n'y arrive pas.
? Merci.
non
tranquilo te donne une piste
pourquoi cette factorisation ? parce que est le module de a
tu dois résoudre :
et sera une mesure de l'argument de a
trouve




